Max Horizontal Force for Block-Wedge Problem

  • Thread starter Thread starter judas_priest
  • Start date Start date
AI Thread Summary
The discussion focuses on determining the maximum horizontal force that can be applied to a block on an incline without causing it to move upwards. Participants clarify the equations used to resolve the force into components, emphasizing the importance of correctly identifying the direction and magnitude of friction. It is noted that as the applied force increases, the frictional force acting against the motion decreases, contrary to initial assumptions. The distinction between maximum static friction and the actual friction force needed to prevent movement is highlighted. Ultimately, the correct approach involves understanding the interplay between the applied force, normal force, and friction to find the maximum force before the block begins to slide.
judas_priest
Messages
174
Reaction score
0

Homework Statement



What is the maximum magnitude of a horizontal Force F that can be applied without causing the block to move up the incline?

Homework Equations





The Attempt at a Solution



Resolving F into it's components and writing down the equations

For x:

Fcos(theta) + μMgcos(theta) = Mg sin(theta)

For y:

Fsin(theta) + mgcos(theta) = N

Are the two equations correct? Because solving for F from this doesn't give me the correct answer.
Where am I going wrong?
 

Attachments

  • block_on_incline.png
    block_on_incline.png
    2 KB · Views: 599
Physics news on Phys.org
Is the direction of Friction correct?
 
You should check the direction and magnitude of friction that you have used. Remember, friction requires the total normal force applied on the body.
 
dreamLord said:
You should check the direction and magnitude of friction that you have used. Remember, friction requires the total normal force applied on the body.

Why is the friction force acting in the direction you think it's acting in? I've added normal force in my equation. Please reason your answers.
 
Static friction is written as \muN, where N is the total normal force on the body. You have written it as \muMgcos(theta).

The direction is correct - I don't know why I asked you check the direction. I meant for you to check the magnitude. Also, does the question say anything about the surface of the wedge? It is possible that they meant for it to be frictionless.
 
dreamLord said:
Static friction is written as \muN, where N is the total normal force on the body. You have written it as \muMgcos(theta).

The direction is correct - I don't know why I asked you check the direction. I meant for you to check the magnitude. Also, does the question say anything about the surface of the wedge? It is possible that they meant for it to be frictionless.

Thanks, you made it clear. Actually, this is the second part of a problem It talks about friction in the first part.

Thank you!
 
judas_priest said:
Thanks, you made it clear. Actually, this is the second part of a problem It talks about friction in the first part.

Thank you!

I think your original expression had the friction in the wrong direction.

To clairify your thinking for me, if the block is about to move up the slope - ie you are at the maximum force asked for - what direction will friction be acting?
 
If we go on increasing the F from 0 to it's correct value, then the OP's direction of friction is correct in my opinion.
 
dreamLord said:
If we go on increasing the F from 0 to it's correct value, then the OP's direction of friction is correct in my opinion.

"What is the maximum magnitude of a horizontal Force F that can be applied without causing the block to move up the incline?"
means what force can be applied when the block is about to move up the slope.
What direction do you think friction will be acting in that case?

If F = 0, the block will (tend to) slide down the slope - friction acting up.

As we increase F, the friction force acting up the slope is reduced until we reach the situation where the block would stay there even on a frictionless slope.

As we increase F further, friction acts down the slope, preventing the block from slipping up the slope.

eventually F will become large enough that the friction is no longer sufficient, and the block will slide up the slope.

The question asks for the maximum F can reach before that slipping happens.

I thus think you are wrong.
 
  • #10
judas_priest said:

Homework Statement



What is the maximum magnitude of a horizontal Force F that can be applied without causing the block to move up the incline?

Homework Equations





The Attempt at a Solution



Resolving F into it's components and writing down the equations

For x:

Fcos(theta) + μMgcos(theta) = Mg sin(theta)

For y:

Fsin(theta) + mgcos(theta) = N

Are the two equations correct? Because solving for F from this doesn't give me the correct answer.
Where am I going wrong?

The applied Force F has a component parallel to the slope (your direction x) which tends to make the block move up the slope, it also has a component perpendicular to the slope (your direction y or -y) which increases the Normal force over the usual Mgcos(θ). and that friction acts in a direction opposed to motion, so in the opposite direction for Fcos(θ) so should have the opposite sign to that term.
 
  • #11
PeterO is right, the static friction opposes the effect of the applied force, to push the block up on the incline. Also, the maximum static friction is μN.

ehild
 

Attachments

  • horforceslope.JPG
    horforceslope.JPG
    18 KB · Views: 484
  • #12
PeterO said:
The applied Force F has a component parallel to the slope (your direction x) which tends to make the block move up the slope, it also has a component perpendicular to the slope (your direction y or -y) which increases the Normal force over the usual Mgcos(θ). and that friction acts in a direction opposed to motion, so in the opposite direction for Fcos(θ) so should have the opposite sign to that term.

Yup, you're right!
Silly mistake.
 
  • #13
PeterO said:
As we increase F, the friction force acting up the slope is reduced

I am having trouble understanding this - should the friction not increase due to increased normal force?
 
  • #14
dreamLord said:
I am having trouble understanding this - should the friction not increase due to increased normal force?

I too was doing it that way. But you're looking at it wrong. The force applied is trying to push the block up. They asked for the maximum force that can be applied before the box starts to move UP. Hence, the frictional force to oppose it from going up, points down.

Needs a little logic. Think for a while. You'll get there.
 
  • #15
dreamLord said:
I am having trouble understanding this - should the friction not increase due to increased normal force?

You are confusing the maximum possible friction, μN, and the actual friction force, which is only ever as big as it needs to be.

eg: 2kg block on a flat surface, μ = 0.3, and let's take g=10 for simplicity here.

μN = 0.3 x 2 x 10 = 6N. ie maximum possible friction is 6N.

If we apply a lateral force of 2N, friction will only be 2N and the block won't move.

Increase the lateral force to 4N, and friction will increase to 4N and the block still won't move

Increase the lateral force to 6N and the friction force increases to 6N and it still doesn't move.

Increase the lateral force further and finally you get some action.

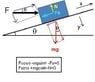
On the slope of your problem, let's suppose the maximum friction available was just enough to stop the block sliding down the slope. The block will thus not move.

once we apply some horizontal force, there will be a component of that force acting up the slope, so although the maximum available friction force will have increased, the magnitude of friction needed will be less, so the friction will reduce.

If the applied force gets big enough, the component of applied Force acting up the slope matches the component of the weight force down the slope so no friction force is needed at all - despite the maximum available friction force being even larger than anything I have written about yet.

If the applied force gets even bigger, the component of applied force acting up the slope will exceed the component of the weight force, so the block will tend to slide up the slope, but the available friction may prevent that slip (by now the available friction is getting quite large)

eventually, if we continue increasing the applied force, the now greater friction force is still not able to prevent the block sliding, so away it goes.
 
  • #16
Ah I get it now. Thank you for the great explanation Peter. Silly thinking on my part - apologies if I caused you any problems OP.
 
  • #17
This is a corrected version with a minus sign:

"Resolving F into it's components and writing down the equations

For x:

Fcos(theta)-μMgcos(theta)=Mgsin(theta)

For y:

Fsin(theta)+mgcos(theta)=N"

May I ask how you can solve for F if you also have N? Two unknowns to my mind. I didn't get it. :(
 
  • #18
Poetria said:
This is a corrected version with a minus sign:

"Resolving F into it's components and writing down the equations

For x:

Fcos(theta)-μMgcos(theta)=Mgsin(theta)

For y:

Fsin(theta)+mgcos(theta)=N"

May I ask how you can solve for F if you also have N? Two unknowns to my mind. I didn't get it. :(
As explained, the frictional force is not μMgcos(theta). It is μN. N is greater than Mgcos(theta) because F contributes to it, as shown in the second equation.
 
  • #19
OK. I got it. Many thanks. :) :) :)
 

Similar threads

Acceleration of a Block Sliding Down a Wedge
Replies
3
Views
849
A block on an accelerating wedge
Replies
4
Views
2K
Block on top of an inclined plane, with a rough surface, that moves with constant acceleration
Replies
41
Views
4K
Calculating the Force Required for a Moving Wedge and Block System
Replies
5
Views
2K
Problem with Dynamic blocks on a fixed inclined plane
Replies
10
Views
2K
Magnitude of force acting on wedge and block
Replies
2
Views
2K
For which case would the applied force be greater?
Replies
41
Views
4K
Block on an accelerating wedge (part c only)
Replies
12
Views
2K
Block and acceleration of wedge
Replies
11
Views
6K
Normal force acting on a block on an accelerating wedge
Replies
12
Views
2K

Hot Threads

Recent Insights

Back
Top