You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
(Boolean Algebra) Did I write this logic expression correctly?
- Thread starter michalodzien
- Start date
AI Thread Summary
The discussion revolves around validating a Boolean algebra expression for homework. The original expression presented was Y=A+((A*B)+B+C'+(B+C'*D)+D), which the poster was unsure about. After feedback, the poster recognized mistakes in parentheses placement and negation for NAND gates, leading to a revised expression F=A+(A*B)+(B*C')+(((B+C')*D)'+D)'. Ultimately, the final simplified expression discussed was C'+A+B, indicating a successful validation of the work.
Physics news on Phys.org
jedishrfu
Mentor
- 15,474
- 10,186
I’d write the intermediate expressions at the gate output and put parentheses around them until you get to the final gate.
Also I’d use the bar over an expression to indicate negation.
Lastly. You can then apply Boolean algebra to reduce the long expression to get your final expression.
Try that and see if you can validate your own work. Doing it with intermediate results helps until you get good at it.
Also I’d use the bar over an expression to indicate negation.
Lastly. You can then apply Boolean algebra to reduce the long expression to get your final expression.
Try that and see if you can validate your own work. Doing it with intermediate results helps until you get good at it.
michalodzien
- 4
- 0
jedishrfu said:I’d write the intermediate expressions at the gate output and put parentheses around them until you get to the final gate.
Also I’d use the bar over an expression to indicate negation.
Lastly. You can then apply Boolean algebra to reduce the long expression to get your final expression.
Try that and see if you can validate your own work. Doing it with intermediate results helps until you get good at it.
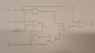
I actually did these parts beforehand but i am not sure if what i came up with is correct and i would like to validate it before i start simplifying it.
Also i have no way to check if it correct because this is for an assignment which i will not get back with feedback but only with a grade.
If you would be so kind to help me on my mistakes and guide me to do this correctly, or just give me the answer i would appreciate it a lot. Either one is fine with me.
Attachments
jedishrfu
Mentor
- 15,474
- 10,186
Your paper is very messy and hard to read.
R = A + B
X = B + C'
Y = ( ( B + C' ) * D )'
Look at the Y gate again.
R = A + B
X = B + C'
Y = ( ( B + C' ) * D )'
Look at the Y gate again.
michalodzien
- 4
- 0
I am sorry for the paper quality.jedishrfu said:Your paper is very messy and hard to read.
R = A + B
X = B + C'
Y = ( ( B + C' ) * D )'
Look at the Y gate again.
I see i did a very silly mistake and forgot to add parentheses around B + C' and ofcourse It's a NAND gate so the expression needs a negation as a whole. I can see i did same mistake with E gate it should have been ((B+C'*D)'+D)'
This is the result i got now:
F=A+(A*B)+(B*C')+(((B+C')*D)'+D)'
It looks correct to me, does it so to you?
jedishrfu
Mentor
- 15,474
- 10,186
Students are always looking for the geodesic when the real geodesic is the step by step approach with intermediate values allowing someone to review it and check each step.
R = A * B (I made a mistake as it was an AND gate)
X = B + C'
Y = ( ( B + C' ) * D )'
E = ( Y + D )' = ( ( ( B + C' ) * D )' + D )'
G = R + X + E = (A * B) + (B + C') + ( ( ( B + C' ) * D )' + D )'
F = A + G = A + (A * B) + (B + C') + ( ( ( B + C' ) * D )' + D )'
Can you check my work?
R = A * B (I made a mistake as it was an AND gate)
X = B + C'
Y = ( ( B + C' ) * D )'
E = ( Y + D )' = ( ( ( B + C' ) * D )' + D )'
G = R + X + E = (A * B) + (B + C') + ( ( ( B + C' ) * D )' + D )'
F = A + G = A + (A * B) + (B + C') + ( ( ( B + C' ) * D )' + D )'
Can you check my work?
michalodzien
- 4
- 0
It all looks correct and i can see this is an easy way to do it, thank you very much for your help!jedishrfu said:Students are always looking for the geodesic when the real geodesic is the step by step approach with intermediate values allowing someone to review it and check each step.
R = A * B (I made a mistake as it was an AND gate)
X = B + C'
Y = ( ( B + C' ) * D )'
E = ( Y + D )' = ( ( ( B + C' ) * D )' + D )'
G = R + X + E = (A * B) + (B + C') + ( ( ( B + C' ) * D )' + D )'
F = A + G = A + (A * B) + (B + C') + ( ( ( B + C' ) * D )' + D )'
Can you check my work?
LCKurtz
Science Advisor
Homework Helper
- 9,567
- 775
Hmmm, I don't check this forum often so I'm a bit late to the party, but I get$$C'+A+B$$when it's all said and done.
Last edited:
Similar threads
- Replies
- 2
- Views
- 2K
- Replies
- 2
- Views
- 2K
- Replies
- 5
- Views
- 6K
- Replies
- 3
- Views
- 2K
- Replies
- 5
- Views
- 2K
- Replies
- 4
- Views
- 2K
- Replies
- 3
- Views
- 3K
- Replies
- 11
- Views
- 2K
- Replies
- 1
- Views
- 3K
- Replies
- 3
- Views
- 2K
Hot Threads
-
Engineering Why is my output current so low in this Transconductance Amplifier cell?
- Started by arhzz
- Replies: 13
- Engineering and Comp Sci Homework Help
-
LTspice: Implementing a Single Balanced BJT Mixer
- Started by SumDood_
- Replies: 17
- Engineering and Comp Sci Homework Help
-
Spiral scissor lift statics
- Started by carlcla
- Replies: 4
- Engineering and Comp Sci Homework Help
-
Engineering Diff gain of a push pull degenerated differential pair
- Started by arhzz
- Replies: 6
- Engineering and Comp Sci Homework Help
-
Engineering AGMA pitting resistance factor of safety (SH)
- Started by ironfalls18
- Replies: 2
- Engineering and Comp Sci Homework Help
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 26
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math