Box on a string, find displacement when first at rest

[lindzzz]

Homework Statement

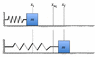
A block with mass m = 3.57 kg is attached to a spring with spring constant k = 165.7 N/m and negligible mass. The coefficient of kinetic friction between the block and the table is µk = 0.239. The box is displaced from its equilibrium position to the left by 0.216 m. If the block is released from rest, calculate the block's displacement when it first comes to rest again.
(Picture attached)

Homework Equations

Us = 1/2kΔL²
Wfriction = μmgdcosθ

The Attempt at a Solution

This is what I tried:
Us = Wfriction
1/2(k)(xf)² - 1/2(k)(xi)² = μmgdcosθ
I then said xf = d - xi and subbed in this for xf
1/2(165.7)(d-0.216)² - 1/2(165.7)(0.216)² = 0.239(3.57)(9.8)d(cos180°)
solving for d I get d = 0.33 m but this is incorrect
I'm not sure what I'm doing wrong, suggestions?

 

[obafgkmrns]

When the block first comes to rest, does the spring exert sufficient force to move the block in the opposite direction. If so, then friction hasn't yet dissipated all the energy initially stored in the spring, and your energy approach won't work. Try solving the equations of motion and calculating the time at which the block comes to rest.

 

[lindzzz]

The reason I'm doing it with energy is that this problem is under the heading: Thermal energy and power. How I see it is if the ground were frictionless then the energy stored in the spring at xi would be equal to that stored at xf, and energy is conserved. However with friction energy will be lost to heat therefore the difference in energy stored in the spring at xf and xi should be equal to the energy lost to heat (friction).

 

[obafgkmrns]

"The reason I'm doing it with energy is that this problem is under the heading: Thermal energy and power."

Got it. You'll have to account for the energy stored in the spring when the block comes to rest:

(Initial Spring Energy) = (Energy Dissipated) + (Spring Energy When Block Stops)

= μmgd + k(d - xi)^2

Actually, that's easier than solving the equations of motion!