yolo123
- 63
- 0
Hi, I have an exam soon. This is urgent. Can you check my answer?
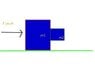
A box with mass 100kg is being pushed with enough force such that a second box with mass 2kg does not slide down and the two accelerate to the right together.
If us=0.5 and uk=0.1, what is acceleration minimum such that box m2 does not slide (please see picture.)? What is minimum value of Fpush?
What would change if block m1 is moving at constant speed?
I find that Fpush minimal is 1915N.
I find that acceleration minimal is 17.8 m/s^2.
If block moves at constant speed, the block would also move at constant speed in x direction but be affected in y direction because of gravity and just fall.
A box with mass 100kg is being pushed with enough force such that a second box with mass 2kg does not slide down and the two accelerate to the right together.
If us=0.5 and uk=0.1, what is acceleration minimum such that box m2 does not slide (please see picture.)? What is minimum value of Fpush?
What would change if block m1 is moving at constant speed?
I find that Fpush minimal is 1915N.
I find that acceleration minimal is 17.8 m/s^2.
If block moves at constant speed, the block would also move at constant speed in x direction but be affected in y direction because of gravity and just fall.