Buoyant force and ambient air pressure

[gloo]

I wanted to inquire as to a thought I have on a situation with buoyancy and air pressure.

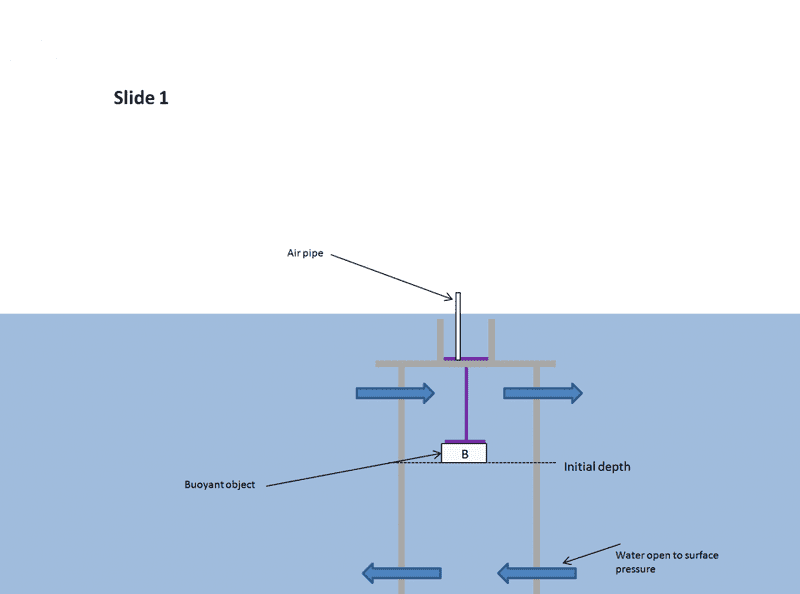
In the first slide (slide 1), I am showing a situation where a buoyant object is pushing up on a support wall through a fixed wall that has water in it. Here are the factors:

1. The net buoyant force of the hollow object is 500 N (pushing upward)
2. The support structure is 300N in weight (purple)
3. The support structure is flush up against the inside of the horizontal walls and do not allow passage of water down
4. The friction is 50N (walls against the support structure horizontal wall; the vertical pole through the bottom fixed wall (grey)

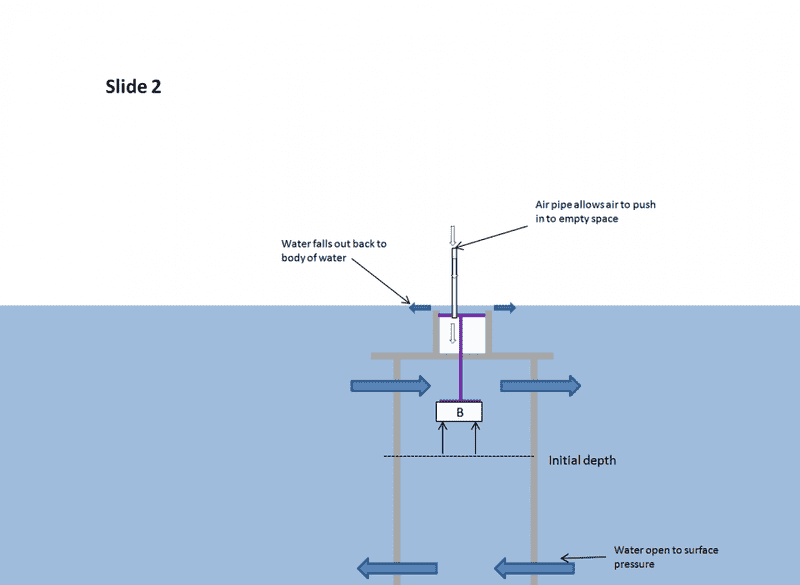
My query is... would this buoyant push from the water below be able to push the water up and out to spill over the sides and back into the main body of water leaving the area below empty with just air? I was thinking it would not need the air pipe to allow air to come in and equalize the air pressure since the air is also pushing down on all the water? But I am wrong? I believe that only with the air pipe will the net force upward (500N up minus (300N + 50N) = 150 N --- would be able to push the water up and out leaving the empty space?

 

[Simon Bridge]

You can see it clearer if you put the setup in a tank... what happens is the overall height of the water increases.
Then you can use conservation of energy to work out what's possible.

 

[gloo]

You can see it clearer if you put the setup in a tank... what happens is the overall height of the water increases.
Then you can use conservation of energy to work out what's possible.

I guess I didn't clarify...but if you look a little more closely, the water will fall back into the body of water because the walls are beneath the surface of the water. I am guessing you mean if the walls were much taller it would raise the water upward?

 

[Simon Bridge]

No - I mean the main body of the water ... assume it is in a tank that has walls that are not pictured.
The small tank on top of the support I get is under water ...

Raising a submerged but buoyant object volume V through height h through water (w) makes energy $\rho_{w}Vgh$ available to do work.
You have a massive piston - so some work is done to lift that.
The water in the small tank where the top of the piston is, that has to be raised enough to reach the top of the tank ... but after that it contributes to the overall height of the main body of water which must be in a container of some kind ... even if that container is the sides of the ocean on a planet or whatever.

You may want to say that the main body of water is so large that the water makes a negligible increase in height ... OK.
But that could be where funny results can come from later.

You may prefer a model where the bottom of the piston is in one tank of water and the top in another ... and the water displaced from the top tank is just lost.
What I am doing is trying to provide you with models to help you work out what is going on.

 

[gloo]

No - I mean the main body of the water ... assume it is in a tank that has walls that are not pictured.
The small tank on top of the support I get is under water ...

Raising a submerged but buoyant object volume V through height h through water (w) makes energy $\rho_{w}Vgh$ available to do work.
You have a massive piston - so some work is done to lift that.
The water in the small tank where the top of the piston is, that has to be raised enough to reach the top of the tank ... but after that it contributes to the overall height of the main body of water which must be in a container of some kind ... even if that container is the sides of the ocean on a planet or whatever.

You may want to say that the main body of water is so large that the water makes a negligible increase in height ... OK.
But that could be where funny results can come from later.

You may prefer a model where the bottom of the piston is in one tank of water and the top in another ... and the water displaced from the top tank is just lost.
What I am doing is trying to provide you with models to help you work out what is going on.

Thanks for the input -- my main query is that :

1. Water is raised up in the small tank
2. Air is replaced below? Without the air pipe...it probably a lot more work because of the air pressure above?

 

[CWatters]

Re the first drawing...Without the air pipe the buoyancy force has to create a vacuum in the top container - so it would have to overcome the head of water in the top container plus atmospheric pressure.

With the air pipe just the head of water.

 

[gloo]

Re the first drawing...Without the air pipe the buoyancy force has to create a vacuum in the top container - so it would have to overcome the head of water in the top container plus atmospheric pressure.

With the air pipe just the head of water.

Re the first drawing...Without the air pipe the buoyancy force has to create a vacuum in the top container - so it would have to overcome the head of water in the top container plus atmospheric pressure.

With the air pipe just the head of water.

So I am a little confused still on what the buoyant force can do. I know there is a buoyant force pushing up on the water in the container. With these following numbers :

Net buoyant force of the hollow object (including weight of materials = 1000N
Weight of purple structure = 200 N
Friction = 20N
Force of water above in container = 4000 N

Can the buoyant force lift up only the volume of water equal to itself (i.e. the volume of empty space )? Or it can't lift any of the water up because the weight of the water is much greater?

 

[Simon Bridge]

When an object is immersed in water, there is an upwards force on it equal to the weight (mg) of the water displaced.
There will also be downwards forces on it - like the weight of whatever the immersed object is made of and the weight of whatever the immersed object is supposed to support.

In your example (above) you have 4200N down and only 1000N up - so, even without friction, the net force is downwards, so float B will sink under the weight.