dropoutofschool
- 3
- 0
View attachment 96628
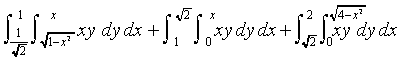
This is the problem I'm trying to solve. The directions require me to rewrite as a single integral and evaluate. But I'm having trouble setting the bounds for a complete compounded integral. The graph of the region would look something like this...
View attachment 96629
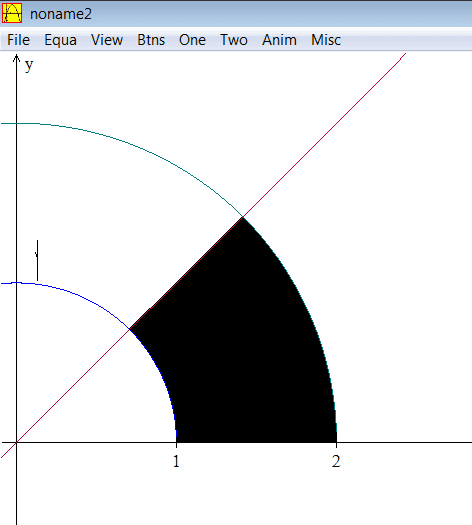
Where the shaded area is the region. I would think its a Type 2 region (dxdy). The y bounds would be 0 to√2 and the x bounds would be from x=sqrt(1-x^2) to x=sqrt(4-x^2)... so so I thought. I then realized that these bounds would extra space outside of the intended shaded region, so the y=x linemust be involved in the bounds somehow.
I just need help setting the integral up, the actual integrating should be easy. Thanks ! Any help is appreciated!
This is the problem I'm trying to solve. The directions require me to rewrite as a single integral and evaluate. But I'm having trouble setting the bounds for a complete compounded integral. The graph of the region would look something like this...
View attachment 96629
Where the shaded area is the region. I would think its a Type 2 region (dxdy). The y bounds would be 0 to√2 and the x bounds would be from x=sqrt(1-x^2) to x=sqrt(4-x^2)... so so I thought. I then realized that these bounds would extra space outside of the intended shaded region, so the y=x linemust be involved in the bounds somehow.
I just need help setting the integral up, the actual integrating should be easy. Thanks ! Any help is appreciated!
Last edited by a moderator: