Calculate angles from infomation given

[sunzone]

Hello :)

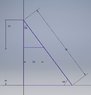
I have a math problem, where I am trying to calculate Q1 (Q2 & Q3) with the info given on the image. I keep telling myself that i need Q2 or/and Q3 to find Q1, but i can't find a formula that i can use

I've drawn it, and found out that Q1 is 10mm, but i can't prove it with math (without drawing)

Is there a kind soul, that know the answer to it, its driving me nuts :)

 

[mfb]

Is this a homework problem?

You can introduce the length of the bottom side as variable, then find two equations depending on this variable and Q1. That should help to determine all lengths and angles.

 

[sunzone]

yes :)

we were told it was unsolvable :)

Thanks, i'll try to see if i can put up an equation :)

 

[mfb]

There is more than one solution, but you can find all solutions.

 

[newjerseyrunner]

I'd break it up into a rectangle and two triangles. The bottom triangle would have side of 14, bottom of L1, and hypotenuse of sqrt(L1^2 + 14^2). Then another triangle with bottom 7.5, side of L2 and hypotenuse of sqrt(L2^2 + 7.5^2);

The sum of the two hypotenuses must equal the hypotenuse of the larger triangle. So 30 = sqrt(L1^2 + 14^2) + sqrt(L2^2 + 7.5^2) = sqrt((L2 + 14)^2 + (L1 + 7.5)^2)).

That should be calculable and from there you can just do the trig.

 

[ElectricRay]

I think the answer will always be some kind of equation? I tried to find a solution but when i made the drawing i started to see that there must be many solution for Q1, Q2 and Q3. Am i right in this or is that only one solution for the 3 variables.

My point of view is that one can rotate the hypotenuse around the horizontal with length 7.5. So there is a boundary for the two right sides of the big triangle due to the 7.5 length. I think the bottem right side must be always > 7.5 and the left ride side must be > 14. Q1 can never be so big that the bottom gets <7.5 etc
How could one state that more mathematically correct? The way i write that here is maybe very confusing.

 

[mfb]

I think the answer will always be some kind of equation?

No, the answers are specific numbers. There is more than one, but the number of solutions is small.

 

[ElectricRay]

I try to figure it out but i get always two unknown variables. This is a fun problem by the way.

And what is a small amount of solutions? 2, 10 or maybe 100? It is surely not infinite that's what i tried to explain in my previous post.

 

[mfb]

And what is a small amount of solutions? 2, 10 or maybe 100? It is surely not infinite that's what i tried to explain in my previous post.

Spoiler

2

And you can find the numbers - although analytic expressions for them are messy as you get a 4th order polynomial.

 

[ElectricRay]

Only so much solutions I am confused now very much. HMMM I would really think i can plug in many real number for L1 and calculate the rest if I would do it the way NewJerseyRunner proposed. When i try to solve it I come on the same equation.