Calculate Change in Momentum of Mass m Launched at 45° Angle

[Victorian91]

Homework Statement

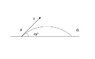
An object of mass m is launched at speed v from point P on horizontal ground at an angle of elevation of 45 degrees, as shown in the picture. When the object reaches point Q the magnitude of the change in momentum of the object is ?

Homework Equations

Change in momentum of the object
mv - mu

The Attempt at a Solution

Honestly, I really don't know how to start
All i know is use the formula of the change of momentum
But then the angle 45 degrees I really don't know where to put..
Can somebody help me

Sorry for not attempting
Is because I am a bit blur..
Lastly the options for this question is

A : Zero
B : 1/2 mv
C : 2mv
D : 4mv

Thanks so much..

 

[Victorian91]

Okay i think I might be able to solve it..
Finally I manage to attempt this question..

Initial velocity, v = ( vcos45 )^2 + ( vsin45 )^2 ( using pythagorean theorum ) ( to find the resultant velocity
Therefore initial velocity = v
Hence, initial momentum, p =mv

Final velocity, v is the same in magnitude but opposite direction,
Hence final momentum, p =-mv

Hence, change in momentum,
is -mv -mv

=-2mv

But the question just wants the magnitude,
Hence = 2mv

Can anybody tell me whether my working is correct??
Thanks

 

[gabbagabbahey]

Final velocity, v is the same in magnitude but opposite direction,

Really? Why do you think that?

Also, momentum is a vector:

\Delta\vec{p}=\vec{p}_f}-\vec{p}_i=m\vec{v}_f}-m\vec{v}_i

What force is causing the momentum to change? Which direction does this force act in? Hence, which component(s) of the momentum change?

 

[Victorian91]

The final velocity of the object will be pointing downwards..
Hence, the it will be the same magnitude as the initial velocity but pointing downwards..

That is what I think..

Is my answer correct?
Or are there any other answers..

Thanks