Victorian91
- 18
- 0
Homework Statement
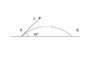
An object of mass m is launched at speed v from point P on horizontal ground at an angle of elevation of 45 degrees, as shown in the picture. When the object reaches point Q the magnitude of the change in momentum of the object is ?
Homework Equations
Change in momentum of the object
mv - mu
The Attempt at a Solution
Honestly, I really don't know how to start
All i know is use the formula of the change of momentum
But then the angle 45 degrees I really don't know where to put..
Can somebody help me
Sorry for not attempting
Is because I am a bit blur..
Lastly the options for this question is
A : Zero
B : 1/2 mv
C : 2mv
D : 4mv
Thanks so much..