-- Calculate force at CG & away from CG

[aschopade29]

Homework Statement

Hello All,

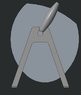
Please help me to find the force required to rotate a body of 4 Kg mass from 0° to 90° in 5 second. this force is acting at center of gravity. (Image: case 1)

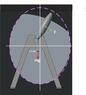
CASE-2: Force acting away from center of gravity. (Image: case 2)

Homework Equations

The Attempt at a Solution

 

[Delta2]

Hi, aschopade29. Welcome to Physics Forums.

You have to upload the images, I believe they are containing crucial info, like what is the shape of the body and where is the centre and the axis of rotation

Also (and this is very important) you have to show us your attempt at a solution before we help you.

 

[aschopade29]

Hi,
I have uploaded the Images
I was tried for CASE-1
Using T= I x α= I x (1/2) Mr² x α
I have substitute this torque in T = F x r
from this get F but I am having doubt on same getting too less F as 1.884 N

CASE-2 : I am not able to relate any equation, I tried with parallel axis theorem but it won't work.

 

[Delta2]

I have trouble understanding the images, I guess our body of interest is the rectangular shaped in red line, but what does the black perimeter line is about?

Also you mean that case 1 is with the axis of rotation passing through the CG right? The force is acting at distance r=50mm from the CG right? Is the direction of the force given ? (I suppose it is always perpendicular to $\vec{r}$?

Case 2 is with the axis of rotation passing through a point that is offset (-20mm,-30mm) from the CG?

 

[aschopade29]

The Black perimeter line is stand or you can say that holding unit on which unit is fixed. The unit is not in rectangular shape, need to consider curvature design.

CASE 1: Your assumption is right, the green lever is attached to unit & its swivel around black periphery.

CASE 2: Right assumption

 

[aschopade29]

Consider these images as referene

 

[Delta2]

Ok now it makes perfect sense
Well first thing we got to know the moment of inertia $I_{CM}$ around the CoM of the body, is this given by the problem?

 

[aschopade29]

No Moment of inertia is not mention in problem
What factors we need to consider while calculating Moment of inertia.

 

[Delta2]

No Moment of inertia is not mention in problem
What factors we need to consider while calculating Moment of inertia.

We need to know the shape and the mass density distribution of the body.

From the 3D images it shows up as some sort of cylindrical slice, maybe we can make the approximation of it as a cylinder..
Anyway we can suppose that we know $I_{CM}$ and proceed with the rest of the problem.

So assuming that the rotation is done with constant force , how did you calculate the constant angular acceleration. There are two ways to calculate it, you should equate the results from the two ways and then solve for the force F (assuming we know the moment of inertia)

 

[BvU]

Perhaps some more revelations are in order: you present two cases, case1 with the center of mass on the axis of rotation, case2 with center of mass 30 mm below and 20 mm forward. That last one should turn all by itself until c.o.m. is below the axis, shouldn't it ?

Are these cases for one and the same device ? Is it a container with moving contents (sand, powder, ...) ?

Then: no one can follow what you did in post #3; please show calculations step by step in complete detail. (but keep the number of digits to a minimum)

And: if the handle is 50 mm long, where do you apply the force ? At the end or in the middle ?

Which way do you want to tumble in reference-1-jpg ? Clockwise or anti clockwise ?

 

[aschopade29]

We need to know the shape and the mass density distribution of the body.

From the 3D images it shows up as some sort of cylindrical slice, maybe we can make the approximation of it as a cylinder..
Anyway we can suppose that we know $I_{CM}$ and proceed with the rest of the problem.

So assuming that the rotation is done with constant force , how did you calculate the constant angular acceleration. There are two ways to calculate it, you should equate the results from the two ways and then solve for the force F (assuming we know the moment of inertia)

For this irregular body how could we found the moment of inertia?

I have calculated angular acceleration as from (theta / time²) that is (1.57 rad/ 5²)=0.0628 rad/sec²
is that correct?

 

[aschopade29]

Perhaps some more revelations are in order: you present two cases, case1 with the center of mass on the axis of rotation, case2 with center of mass 30 mm below and 20 mm forward. That last one should turn all by itself until c.o.m. is below the axis, shouldn't it ?

Are these cases for one and the same device ? Is it a container with moving contents (sand, powder, ...) ?

Then: no one can follow what you did in post #3; please show calculations step by step in complete detail. (but keep the number of digits to a minimum)

And: if the handle is 50 mm long, where do you apply the force ? At the end or in the middle ?

Which way do you want to tumble in reference-1-jpg ? Clockwise or anti clockwise ?

Thanks for reply

Yes, the case is same for the device. the container contain material having approx weight 500 g (but for now calculating for empty).

I am applying force in the middle (as hand gripping is there so considered middle)

I want to tumble in clockwise.

 

[aschopade29]

Thanks for your replies,

Please let me know if I need to start in another directions or else what Input I need to consider else from mention, so I will try to figure out.

 

[Delta2]

For this irregular body how could we found the moment of inertia?

I have calculated angular acceleration as from (theta / time²) that is (1.57 rad/ 5²)=0.0628 rad/sec²
is that correct?

Almost, the correct equation is $\theta=\frac 1 2 at^2$ so essentially you have to multiply your 0.0628 result by 2.
How can you calculate $a$ from $T=I_{CM}\cdot a$ assuming we know $I_{CM}$?

 

[BvU]

So, to recap: you have a 4 kg container some 100 mm wide (if the drawing is to scale) and 110 high. and some 60 mm in the z direction.
A containder isn't solid

You want to rotate over $\pi/ 2$ clockwise around an off-center axis. By exerting a force F at 25 mm from the axis of rotation.

I drew a pink ellipse around the thing: the center of mass will be lower and to the right of the intersection of the white symmetry axes, due to the missing bit top right -- and the material in the z-direction being mostly below the white line.

Your force F doesn't just have to let the thing rotate, it will also have to compensate the torque from mg, so things become complicated !