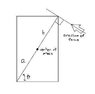
flfgw said:
Thank you so much. Youve been a great help! Yes i did mean that a is the length of the diagonal between the lower corner and the cm. I also did mean (a+b). I am sorry but even with your help I am still not quite certain how this formula was ascertained. Could you please try to explain it.
OK, let's look specifically at this sample problem, not at your problem statement. By looking at the sketch, you should be able to visualize that the block will ultimately tip about the lower left hand corner (the pivot point, where the normal force betwen the ground and the block will be concentrated at the critical 'tipover' force) when you apply a certain force , F, at the top. The force, F, will produce a counterclockwise torque about the pivot. The block's weight, concentrated at the c.m., will produce a clockwise torque about that pivot. When these two torques are equal, the block will just be on the verge of tipping. Thus , set the two torques equal, and solve for F. From the definition of torque, the torque from the weight, mg, is (weight times perpendicular distance from the line of action of the weight force to the pivot). Thus, using a little trig, it's torque is mg(a)cos\theta, clockwise . (Alternatively, using the second definition for torque I noted earlier, you get the same result, mg(a)sin(\theta -90), which is equivalent to mg(a)cos\theta). Now in a similar fashion, the torque from the force , F, is F(a+b), counterclockwise. Set these 2 torques equal, and solve for F, thus, mg(a)cos\theta = F(a+b), or F = mg(a)cos\theta/(a+b). Now admittedly, this is the case where F is applied at a right angle to the diagonal, which gives the minimum force required. This might be a bit difficult to see. If for example F were applied horizontally at the top, instead of at an angle, it's value would be larger to give the same torque. Now your problem is a little harder, because the c.m. is not at the center of the rectangle. But use the same approach: and note that the line of action of the the force should be perpendicular to the pivot to get the minimum force required.