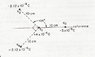
Bama
- 15
- 0
Ok, here is what I have. See attachment to complete the problem.
What is the magnitude of force exerted on charge q1 by charge q3 and horizontal component of force exerted?
Formula: q1q2 / 4piEor^2
Part 1) (4*10^-6)(2.12*10^-6) / 12.56 (8.85*10^-12)(1*10^-2) = 7.628917917176 N or Rounded off as 7.63N
Part 2) 7.63 N sin 135 degrees = 5.39 N
Now I understand the above, howver what I can understand is the following. The resultant force exerted on the charge q1 by the other 3 charges is what? But what if we replaced q1 with charge -4*10^-6, what resultant force would be exerted by the other 3 charges?
What is the magnitude of force exerted on charge q1 by charge q3 and horizontal component of force exerted?
Formula: q1q2 / 4piEor^2
Part 1) (4*10^-6)(2.12*10^-6) / 12.56 (8.85*10^-12)(1*10^-2) = 7.628917917176 N or Rounded off as 7.63N
Part 2) 7.63 N sin 135 degrees = 5.39 N
Now I understand the above, howver what I can understand is the following. The resultant force exerted on the charge q1 by the other 3 charges is what? But what if we replaced q1 with charge -4*10^-6, what resultant force would be exerted by the other 3 charges?