Calculate moment of a special wrench

[jonjacson]

Homework Statement

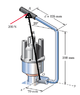
The specialty wrench shown in the figure is designed for access to the hold-down bolt on certain automobile distributors. For the configuration shown where the wrench lies in a vertical plane and a horizontal 200-N force is applied at A, perpendicular to the handle, calculate the moment applied to the bolt at O. For what value of the distance d would the z-component of be zero?

Homework Equations

M = r x F ;

M= Fd

The Attempt at a Solution

Well I succesfully calculated the moment around O as M=-48.6j -9.49k Nm but I failed to calculate the second part of the problem.

It was asking for d in order to make Mz equal to zero.

Using M=Fd I have:

M=√My²+Mz² = F d

From that equation I have to find d in order to make Mz zero so I substitute Mz for zero and I calculate te value of d:

√My²=Fd

d=My/F=48.6/200=0.24

But the book gives a value of 74.5 mm, What am I doing wrong?

Thanks!

 

[voko]

You could solve this in two different ways. First, you could express r as a function of d, then use the M = r x F to find the dependence on d.

Or, you could recall that the moment about an axis is proportional to the distance from the axis.

 

[jonjacson]

You could solve this in two different ways. First, you could express r as a function of d, then use the M = r x F to find the dependence on d.

Or, you could recall that the moment about an axis is proportional to the distance from the axis.

Ohh, I´m sorry, you are right. I was assuming that d was the moment arm but it´s not, in this problem is the distance d as it´s shown in the picture, what a ridiculous mistake.

Now I find the correct answer:

d=70/cos(20)=74,5 mm

Thank you very much!