MathewsMD
- 430
- 7
60. A ship’s anchor weighs 5000 N. Its cable passes over a roller of negligible mass and is wound around a hollow cylindrical drum of mass 380 kg and radius 1.1 m, mounted on a frictionless axle. The anchor is released and drops 16 m to the water. Use energy considerations to determine the drum’s rotation rate when the an- chor hits the water. Neglect the cable’s mass.
Solution:
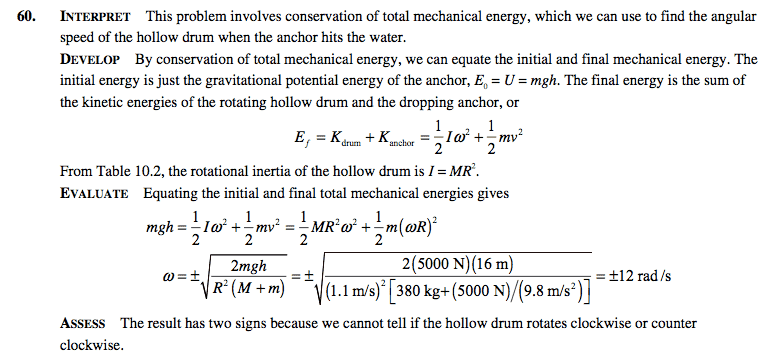
Under "Evaluate" they say the kinetic energy of the anchor is 1/2m(ωR)2 but why do we assume R to be the radius of the cylinder and why do we consider the angular velocity of both the cylinder and anchor to be the same? Why can't the angular velocities be different? I may be visualizing it incorrectly, but I am slightly confused on why we assume R and ω to be the same for both the anchor and cylinder when they are not even in contact anymore.
Solution:
Under "Evaluate" they say the kinetic energy of the anchor is 1/2m(ωR)2 but why do we assume R to be the radius of the cylinder and why do we consider the angular velocity of both the cylinder and anchor to be the same? Why can't the angular velocities be different? I may be visualizing it incorrectly, but I am slightly confused on why we assume R and ω to be the same for both the anchor and cylinder when they are not even in contact anymore.