- #1
jonjacson
- 447
- 38
Hi to everybody
(The attachment has an image with this problem)
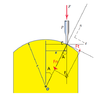
A small probe P is gently forced against the circular surface with a vertical force F as shown. Determine the n- and t-components of this force as functions of the horizontal position s.
Newton laws and basic trigonometric relationships.
Well I show in the attachment my reasoning, the force F is applied at the contact point C, I have represented the direction in which this force acts (vertical line). I need to find the proyections of F to the n and t axis, to calculate Fn and Ft in red.
Well I think that the angle between the vertical line and the line connecting the center O and the point C is the same angle between F and Fn, in the picture they are called A. I simply write:
Fn= F cos(A)
Ft= F sen(A)
And I can calculate A as:
A=arcsen(s/r)
But I have seen the answers provided in the book and they are:
Ft=Fs/r
and
Fn= -(F√(r2-s2))/r
Does anybody know what is Fs?
And I have no idea where the equation for Fn comes from.
Why are my answers so different to the ones in the book?
Thank you
Homework Statement
(The attachment has an image with this problem)
A small probe P is gently forced against the circular surface with a vertical force F as shown. Determine the n- and t-components of this force as functions of the horizontal position s.
Homework Equations
Newton laws and basic trigonometric relationships.
The Attempt at a Solution
Well I show in the attachment my reasoning, the force F is applied at the contact point C, I have represented the direction in which this force acts (vertical line). I need to find the proyections of F to the n and t axis, to calculate Fn and Ft in red.
Well I think that the angle between the vertical line and the line connecting the center O and the point C is the same angle between F and Fn, in the picture they are called A. I simply write:
Fn= F cos(A)
Ft= F sen(A)
And I can calculate A as:
A=arcsen(s/r)
But I have seen the answers provided in the book and they are:
Ft=Fs/r
and
Fn= -(F√(r2-s2))/r
Does anybody know what is Fs?
And I have no idea where the equation for Fn comes from.
Why are my answers so different to the ones in the book?
Thank you