MattDutra123
- 15
- 0
- Homework Statement
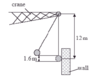
- A solid iron ball of mass 770kg is used on a building site. The ball is suspended by a rope from a crane. The distance from the point of suspension to the centre of mass of the ball is 12m. The ball is pulled back from the vertical and then released. It falls through a vertical height of 1.6m and strikes a wall. Calculate the tension in the rope just before impact.
- Relevant Equations
- F (centripetal force) = mv^2/r
The solution to the problem simply states: "Use of mv^2/r = 2000. T = (2000 + 7500) = 9500N". I don't understand this solution. Nothing more is provided. I don't know how you are supposed to find the radius (in order to use the centripetal force formula) merely from the information provided. Also, why is the tension the sum of the centripetal force and weight (7500)?
Can someone please explain this to me?
The problem provides a sketch. I have included it in the attachments.
Can someone please explain this to me?
The problem provides a sketch. I have included it in the attachments.