swirly90
- 8
- 0
1. How long will it take a plane to travel 100km [N] if its ground velocity is 796km/h [25 W of N]
I am having the hardest time with question since I actually don't know how to start. I know it require the fomula T= V*D. I manage to get a diagram but that is far as I gone. =(
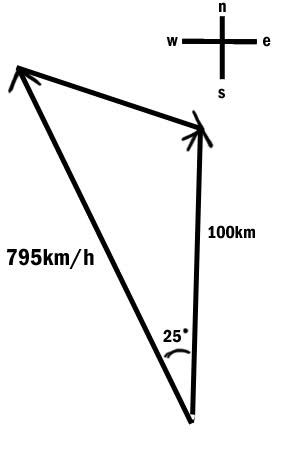
Help? I have a final tomorrow and I need to able to do this kind of questions.
I am having the hardest time with question since I actually don't know how to start. I know it require the fomula T= V*D. I manage to get a diagram but that is far as I gone. =(
Help? I have a final tomorrow and I need to able to do this kind of questions.