Vectors - Aircraft's velocity relative to ground

[g9WfI]

Homework Statement

An aircraft is scheduled to fly from London to Belfast, a distance of 510 km in a direction N 40 W. The aircraft has a cruising speed of 240 m/s in still air. On the day of the flight, there is a wind of velocity 15 m/s towards the east. Find the direction in which the aircraft must fly to reach Belfast without any change of course, and the magnitude of the velocity of the aircraft relative to the ground.

Relevant Equations

relative velocities, cosine rule, sine rule

I attach my working below - my angle is correct according to mark scheme but magnitude isn't (should be 230).
I think it's odd that my resultant velocity on a windy day is larger than velocity in still air, but apparently my angle is correct?

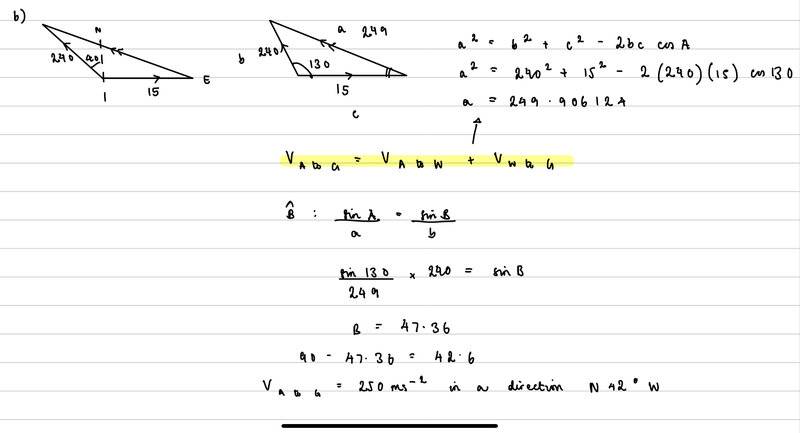
I've been told that I've calculated the airspeed it would need if it were to maintain a ground speed of 240 m/s... And the question asked for the ground speed given that the airspeed is 240.

I don't fully understand the above statement. Is the highlighted equation in my working correct? How do I change my vector diagram? At the moment, I can't see any other way to use the information given.

It appears I just don't know how to do this q - I haven't seen an example like this before. I'd be so grateful for any help.

 

[haruspex]

Your diagrams are wrong.
You have two vectors emanating from the same point, then draw the resultant as connecting their endpoints.
Instead, you can use either of the following:
1. Nose to tail: Draw one vector from point O to point A, and the second vector from A to B. The resultant is then OB.
2. Complete the parallelogram: Draw one vector from O to A and the second from O to B. Now draw AC and BC so that OACB is a parallelogram. The resultant is OC.

It will help if you draw the magnitude 240 vector longer than the magnitude 15 vector!

 

[skeeter]