ahello888a
- 23
- 0
Venturi meter help!
A venturi meter is measuring the flow of water; it has a main diameter of 3.0 cm tapering down to a throat diameter of 1.0 cm. If the pressure difference is measured to be 16 mmHg, what is the speed of the water entering the venturi throat?
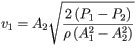
Got that equation from a previous part of the problem where it asked me to "Show that the flow speed measured by a venturi meter (see Figure 13–32 in the textbook) is given by the relation"
I used \rho to be density of water. I converted the diameters to radius in meters. I converted the pressure to "m-Hg". I get 1.77*10^-5. The homework program keeps telling me I'm wrong. I can't see what I'm doing wrong. Thank You for the help!
Homework Statement
A venturi meter is measuring the flow of water; it has a main diameter of 3.0 cm tapering down to a throat diameter of 1.0 cm. If the pressure difference is measured to be 16 mmHg, what is the speed of the water entering the venturi throat?
Homework Equations
Got that equation from a previous part of the problem where it asked me to "Show that the flow speed measured by a venturi meter (see Figure 13–32 in the textbook) is given by the relation"
The Attempt at a Solution
I used \rho to be density of water. I converted the diameters to radius in meters. I converted the pressure to "m-Hg". I get 1.77*10^-5. The homework program keeps telling me I'm wrong. I can't see what I'm doing wrong. Thank You for the help!