Calculating Acceleration and Tension in a Pulley System on an Inclined Plane

[squintyeyes]

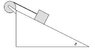
A mass is placed on a frictionless incline and attached to a pulley by a light string. The situation is sketched below.



The incline angle, theta, is 42.0°, the mass is 3.00 kg, the moment of inertia of the pulley is 0.400 kgm2 and the radius of the pulley is 0.145 m. The mass is released from rest.

(a) What is the magnitude of the acceleration of the mass?
___________m/s2
(b) What is the magnitude of the angular acceleration of the pulley?
___________rad/s2
(c) What is the tension in the string?
___________ N


Attempt
T =tension in the string which opposes mass
weight perpendicular to ramp = mgsinθ
a= linear acceleration
mgsinθ-T=ma

Iα=T*r(Because force on pulley is tension T and distance from center of pulley is r)

α=a/r

T=Iα/r=Ia/r2

substituting in
mgsinθ-Ia/r2=ma
mgsinθ=a(m+I/r2)
a=mgsinθ/(m+I/r2)=0.8931m/s2

b)α=0.9/0.145=6.1599rad/s2
c)T=Ia/r2=0.4*0.9/(0.145)2=17N

can someone who knows what they are doing look this over and fix any mistakes.
Please i really need this.

 

[Dick]

That seems ok to me.

 

[tiny-tim]

Welcome to PF!

Hi squintyeyes! Welcome to PF!

(I haven't checked your arithmetic , but apart from that I agree with Dick) your formulas are fine.

 

[squintyeyes]

but my answers are marked wrong and i am down to my last try

 

[tiny-tim]

(just got up :zzz: …)

but my answers are marked wrong and i am down to my last try

hmm … it would have helped if you'd said that at the start.

well, I've looked at it again, including the arithmetic, and I can't see what's wrong.

Which parts are marked right, and which wrong?

How many sig figs are you supposed to enter? how many did you enter?

Are you supposed to use g = 9.8 or 9.81?

Are you sure it says "radius", not "diameter"?

 

[squintyeyes]

Thanks for looking at this. I plugged the first two answers to three decimal places and got them both wrong and it says radius not diameter. I am lost. Thanks again