Calculating Charge for Replacing a Power Supply in an Electric Field Experiment

[CaptCakey]

Homework Statement

In lab we did an experiment where there was a 12v D.C. power supply in a glass dish filled with water. We set the + and - terminals in the dish and a piece of graph paper underneath. With a volt-meter we hunted for certain electric potentials such as 2V, 4V, 0V, etc and wrote down the co-ordinates. This was then plotted, and we were told to draw the electric field. Basically a dipole. No big deal.

Then the professor offered us a lucrative opportunity for extra-credit which I can't resist because the class is difficult and I want to learn how to do things like this. The question is: For what charge Q could replace the 12V power source. This was all fine and dandy but I am sure I've made a mistake somewhere in my math. Not asking for an answer by the way. Any hints or ideas would be greatly appreciated!

Homework Equations

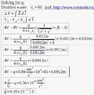
∇V = -E

The Attempt at a Solution

See attached files.

Edit by the way: I only show my result for the i vector componant because I did the Y similarly. I later took the magnitude of the resultant q vector for my answer.

 

[member 553083]

I used the equation ∇V = -E, and solved for q. q = (1/2πε)∫[∇V]dAWhere V is the potential, E is the electric field, ε is the permittivity of free space, q is the charge, and dA is the area of the graph paper.I then took the integral of the electric field in each direction (i and y) and multiplied it by the area of the graph paper. This gave me the total charge of the power source. I then divided this by 12v to get the charge Q.