Calculating Composite Center of Gravity -- Boat Rack for my Truck

[RLewis42]

Hi, I'm new here, great forum!

I am building a boat rack for the top of my truck for a particular boat and boat dolly. The boat will be upside down with the beach dolly attached. It is a side loader, so balance is critical. I need to calculate the combined Center Of Gravity (COG) of the boat and dolly before I will have them together to be able to measure it with a hoist. I have come up with a common sense equation for this, but sometimes in physics things that you think are simple and linear are not. Thanks for any information. I don't know if it is the correct term, but I am using COG as the balance point of an object when the fulcrum is placed below the object.

First, I have a rudimentary question about COG that may seem ridiculous, but this is not my field and I do not assume I know anything until I know it.

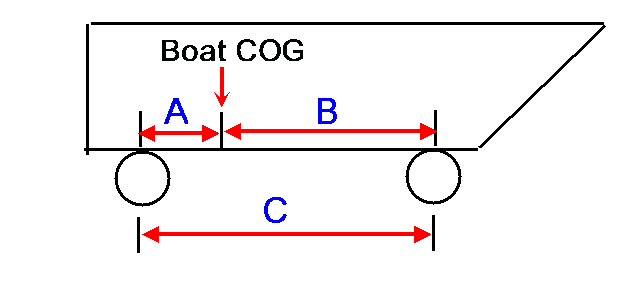
If I want 75% of the boat weight to be on the rear axle, do I place the Boat COG 25% of the wheelbase(C) ahead of the rear axle?

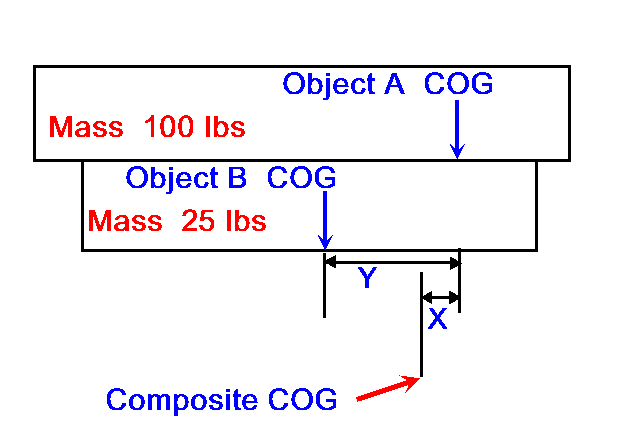
Now for the composite part. Two objects A and B are stacked and I need to calculate the combined COG of the stack. Obviously, the combined COG will fall somewhere between the two object COGs. Can I calculate the distance (x) that the combined COG moves away from the Object A COG as (Y)*(MassB/MassA) ? In this example it would be Y/4.

 

[Simon Bridge]

In this example it would be Y/4.

No. You need the torques to balance - so if X is the moment arm for object A, then Y-X is the moment arm for object B.

Similar for the first question - you need the force on the rear axle due to the torque about the front axle to be 1/4 of the overall weight.

 

[RLewis42]

Simon,

Thanks very much for helping.

I am not sure where to go from here. Let's look at the two examples separately.

1. Placing Boat on Trailer: Let's say I have taken a 2" wide sling around the bottom of the 14' boat and hoisted upward to determine the point on the boat where it balances. I have been calling this COG. If I want 75% of the weight of the boat on the rear axle, the trailer wheelbase is 10'. Are you saying it is not as simple as moving the boat COG 2.5' ahead of the rear axle? Is it close? What else could I do?

2. Composite COGs: You say that my simple attempt to calculate the new COG ignores torque. Do you mean that the approximate new COG cannot be determined with the given data? For example, are you saying that when the top object A's fulcrum is moved downward under object B that the original COG of object A is useless information and cannot help determine the new composite COG?

thanks,

 

[Simon Bridge]

Are you saying it is not as simple as moving the boat COG 2.5' ahead of the rear axle?

That is correct - something you can verfy by building a small model and experimenting.

Is it close?

Define "close".

What else could I do?

You could work out the center of gravity correctly ;)

You say that my simple attempt to calculate the new COG ignores torque.

Did I? I didn't mean to.
The objects have a lot of symmetry so finding the balance point will find you the axial location of the COG - you don't care how high the point is off the axis so that should be fine for your purposes. The "balance point" automatically accounts for the torques - I am saying that your approach to finding the composite COG is incorrect - you need to modify it as I have said to.

Do you mean that the approximate new COG cannot be determined with the given data?

No.
I mean that it's your boat/trailer and if you don't want to pay an engineer you'll just have to learn to do it yourself.

If you have mass A and mass B separated by a distance y, then the COG will be at distance x from mass B that satisfies the relation:
$\qquad$ m_A(y-x)=m_Bx
... solve for x.

Do you not know how to calculate COG and moments?

 

[RLewis42]

Thanks Simon for your help and patience.

1. Composite COGs:

For Ma = 100 lbs, Mb = 25 lbs, y = 10, I see the equation you suggest, mA(y-x)=mBx, gives a significantly different answer (8) than my proposed formula: (Y)*(MassB/MassA) which gives (7.5).

Thanks for that correction.

2. Placing Boat on Trailer:

Below, I have tried to adapt some moment COG equations to my problem.

Example: W = 300 lbs S = 8' want to find s1 and s2 for 75% of W on rear axle:

R1 * s1 = R2 * s2

R1 = .75 * 300 = 225

R2 = .25 * 300 = 75

225 * s1 = 75 * s2

s1 = 75/225 * s2 = .333 * s2

s1 + s2 = 8'

(.333 * s2) + s2 = 8'

s2 * (.333 + 1) = 8'

s2 * 1.333 = 8'

s2 = 6 s1 = 2

Is this correct? What puzzles me is that it the same answer as given by my intuitive "Bubba Science" formula:

s2 = S * (% of W you want on rear axle)

thanks for any clarification,

 

[jack action]

Everything above is right (except m_A(y-x)=m_Bx should read m_B(y-x)=m_Ax according to the drawing) but here's a more direct approach:

The summation of moment (a.k.a. torque) about any point should be equal to zero. Since we can use any point of reference, we can choose the point where the front reaction force is applied. This will eliminate this force as its moment about this point is zero (no lever arm). So the other two moments will have to balance out:

W * S2 = R1 * S

Or:

R1 / W = S2 / S

And because R1 / W is the %W on the rear axle by definition, then S2 / S represent the same value.

Then you can simply find the other values by substraction, i.e. S1 = S - S2 and R2 = W - R1.

Composite COG

For the composite COG, you can use a similar thinking. You choose the point of reference to be acting at one of the mass COG, say m_A. Then, all that is left are the reaction moment of the total weight and the one from W_B = m_Bg. So:

(m_A + m_B)g * x = m_Bg * y

g can be eliminated:

(m_A + m_B) * x = m_B * y ----------> note that it is the same as m_B(y-x)=m_Ax

Or:

x = m_B / (m_A + m_B) * y
x = m_B / m_total * y