- 4,796
- 32
I have this assignement (due tomorrow by the way) where I must compare the range of a projectile on the non-rotating Earth with the range of the projectile on the rotating earth. The question reads:
For a rotating system at the surface of the earth, the equation of motion in the rotating coordinate system reads (Symon pp. 278 equ. 7.36)
m\frac{d^{*2}\vec{r}}{dt^2}= \vec{F} - m\vec{\omega}\times(\vec{\omega}\times\vec{r})-2m\vec{\omega}\times\frac{d^{*}\vec{r}}{dt}-m\frac{d\vec{\omega}}{dt}\times\vec{r}
We neglect terms containing \omega^2. This means we can neglect the centripetal force in the above equation. And the rotation of the Earth is constant so the last term vanishes too.
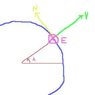
I chose a coordinate system located at the surface of the Earth and whose 3 axis points towards nord, east and vertical, each equiped with unit vectors respectively \hat{n}, \hat{e} and \hat{v}
I find that the angular speed is
\vec{\omega} = \omega cos\lambda \ \hat{n} + \omega sin \lambda \ \hat{v}
My dilemna lies in that by calculating the coriolis force, I get
-2\omega \left[ \left(cos \lambda \frac{d^*v}{dt}-sin\lambda \frac{d^*n}{dt} \right) \hat{e}-cos\lambda \frac{d^*e}{dt}\ \hat{v}+sin\lambda \frac{d^*e}{dt}\ \hat{n}\right]
So solving the equation of motion for either e(t), v(t) or n(t) would means solving 3 second order D.E. simultaneously! I doubt this is what is asked of me in this introductory course to special relativity (!)… On the other hand, my friend is convinced, though he cannot explain why, that the term d^*\vec{r}/dt in the coriolis force is to be taken as the speed function for a regular projectile, that is
\frac{d^*\vec{r}}{dt} = (v_0 cos \alpha)\hat{e} + (v_0 sin \alpha - gt)\hat{v}
So either way, it makes no sense to me. Please tell me what you think.
I asked the teacher and he said that the range is rather small, so we can consider the Earth locally flat.A projectile is lauched towards east from a point located north of the equator at the geographical latitude \lambda. Its initial speed v_0 makes and angle \alpha with respect to the ground. If the range of the projectile is R for \omega = 0, calculate the change in range cause by the rotation of the earth. Neglect terms of order \omega^2.
For a rotating system at the surface of the earth, the equation of motion in the rotating coordinate system reads (Symon pp. 278 equ. 7.36)
m\frac{d^{*2}\vec{r}}{dt^2}= \vec{F} - m\vec{\omega}\times(\vec{\omega}\times\vec{r})-2m\vec{\omega}\times\frac{d^{*}\vec{r}}{dt}-m\frac{d\vec{\omega}}{dt}\times\vec{r}
We neglect terms containing \omega^2. This means we can neglect the centripetal force in the above equation. And the rotation of the Earth is constant so the last term vanishes too.
I chose a coordinate system located at the surface of the Earth and whose 3 axis points towards nord, east and vertical, each equiped with unit vectors respectively \hat{n}, \hat{e} and \hat{v}
I find that the angular speed is
\vec{\omega} = \omega cos\lambda \ \hat{n} + \omega sin \lambda \ \hat{v}
My dilemna lies in that by calculating the coriolis force, I get
-2\omega \left[ \left(cos \lambda \frac{d^*v}{dt}-sin\lambda \frac{d^*n}{dt} \right) \hat{e}-cos\lambda \frac{d^*e}{dt}\ \hat{v}+sin\lambda \frac{d^*e}{dt}\ \hat{n}\right]
So solving the equation of motion for either e(t), v(t) or n(t) would means solving 3 second order D.E. simultaneously! I doubt this is what is asked of me in this introductory course to special relativity (!)… On the other hand, my friend is convinced, though he cannot explain why, that the term d^*\vec{r}/dt in the coriolis force is to be taken as the speed function for a regular projectile, that is
\frac{d^*\vec{r}}{dt} = (v_0 cos \alpha)\hat{e} + (v_0 sin \alpha - gt)\hat{v}
So either way, it makes no sense to me. Please tell me what you think.
Last edited: