ussername
- 60
- 2
Let's suppose an electrochemical system with given coordinates:
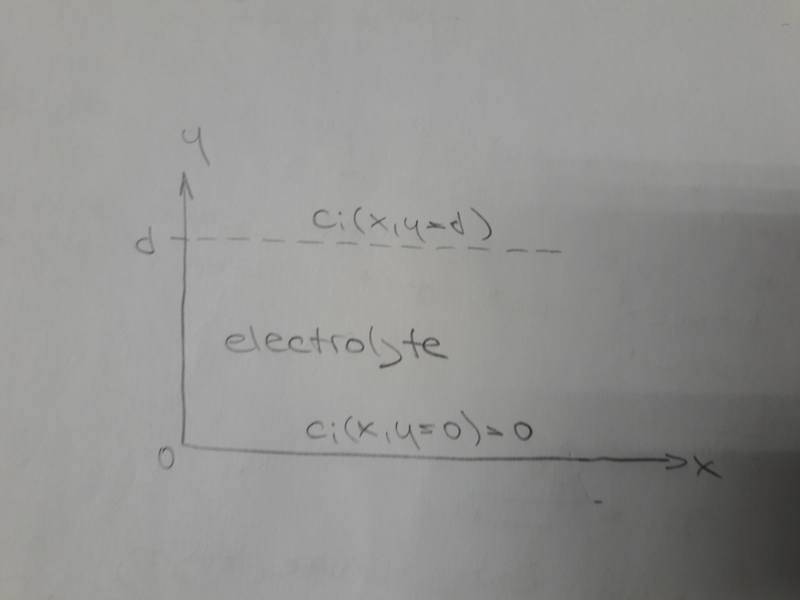
We are interested in diffusion motion of ion ##i## in the direction of ##y## axis.
Concentration ##c_i## is a function of both ##x## and ##y##. Concentration ##c_i## at ##y=0## is zero.
The system is steady thus ##\frac{\partial c_i}{\partial y}(x)## is not a function of ##y## (##\frac{\partial c_i}{\partial y}(x)## is constant with ##y##).
The first Fick's law for ion ##i## is (for simplicity I don't write ##i## subscript anymore):
$$J_{y}^{dif}(x,y=d) = - D \cdot \frac{\partial c}{\partial y}(x,y=d) = - D \frac{c(x,y=d)}{d}$$
The diffusion molar flux is:
$$J_{y}^{dif}(x,y=d) = c(x,y=d)\cdot v_{y}^{dif}(x,y=d)$$
where ##v^{dif}## is the diffusion linear velocity of ion ##i##:
$$v_{y}^{dif} = -D \cdot \frac{1}{c}\cdot \frac{\partial c}{\partial y}$$
The diffusion velocity clearly changes because concentration changes with ##y##.
Now I can put the diffusion velocity into the first equation and express ##D##:
$$D = \frac{-c(x,y=d)\cdot v_{y}^{dif}(x,y=d)\cdot d}{c(x,y=d)}=-v_{y}^{dif}(x,y=d)\cdot d$$
This seems strange to me. Since both diffusion coefficient ##D## and length ##d## are considered constant, the diffusion velocity ##v_{y}^{dif}(x,y=d)## seems to be constant along ##x## independently of the functions ##c(x) \ at \ y=d## and ##\frac{\partial c}{\partial y}(x) \ at \ y=d##. Is it true?
We are interested in diffusion motion of ion ##i## in the direction of ##y## axis.
Concentration ##c_i## is a function of both ##x## and ##y##. Concentration ##c_i## at ##y=0## is zero.
The system is steady thus ##\frac{\partial c_i}{\partial y}(x)## is not a function of ##y## (##\frac{\partial c_i}{\partial y}(x)## is constant with ##y##).
The first Fick's law for ion ##i## is (for simplicity I don't write ##i## subscript anymore):
$$J_{y}^{dif}(x,y=d) = - D \cdot \frac{\partial c}{\partial y}(x,y=d) = - D \frac{c(x,y=d)}{d}$$
The diffusion molar flux is:
$$J_{y}^{dif}(x,y=d) = c(x,y=d)\cdot v_{y}^{dif}(x,y=d)$$
where ##v^{dif}## is the diffusion linear velocity of ion ##i##:
$$v_{y}^{dif} = -D \cdot \frac{1}{c}\cdot \frac{\partial c}{\partial y}$$
The diffusion velocity clearly changes because concentration changes with ##y##.
Now I can put the diffusion velocity into the first equation and express ##D##:
$$D = \frac{-c(x,y=d)\cdot v_{y}^{dif}(x,y=d)\cdot d}{c(x,y=d)}=-v_{y}^{dif}(x,y=d)\cdot d$$
This seems strange to me. Since both diffusion coefficient ##D## and length ##d## are considered constant, the diffusion velocity ##v_{y}^{dif}(x,y=d)## seems to be constant along ##x## independently of the functions ##c(x) \ at \ y=d## and ##\frac{\partial c}{\partial y}(x) \ at \ y=d##. Is it true?
