Calculating Distance for Jumping off a Slope at 45°

  • Thread starter Thread starter borovecm
  • Start date Start date
  • Tags Tags
    Trajectory Urgent
Click For Summary
SUMMARY

The discussion focuses on calculating the distance a jumper travels when launching off a slope at a 45-degree angle with an initial speed of 20 m/s and a launch angle of 15 degrees. The relevant equations for this problem include horizontal distance (x = Vox * t) and vertical distance (y = Voy * t - 1/2 * g * t^2). The user expresses difficulty in starting the problem, particularly in adapting their knowledge from a similar scenario involving a projectile launched from a building at a 30-degree angle.

PREREQUISITES
  • Understanding of projectile motion principles
  • Familiarity with kinematic equations
  • Knowledge of trigonometric functions for angle calculations
  • Basic grasp of gravitational acceleration (g = 9.81 m/s²)
NEXT STEPS
  • Study the derivation of projectile motion equations
  • Learn how to resolve initial velocity into horizontal and vertical components
  • Explore the impact of launch angles on projectile trajectories
  • Investigate the effects of different slopes on projectile motion
USEFUL FOR

Students studying physics, particularly those focusing on mechanics and projectile motion, as well as educators seeking to explain the concepts of angle and distance in real-world applications.

borovecm
Messages
13
Reaction score
0

Homework Statement



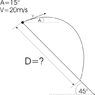
I have to calculate disctance that body(for example a jumper) that jumps of a slope at 45 degrees with initial speed of 20 m/s and under 15 degrees.

Homework Equations


x=Vox * t
y=Voy*t - 1/2*g*t*t

y=ax + b, b=0 => y=ax
-

The Attempt at a Solution



I don't know where to start. I can solve a simillar example where body has been shot from a building with a certain initial speed and under under 30°. It is simillar to this picture, but here it is difference that we shoot from a slope and we don't know at what height we only know that slope is placed under 45° with a surface.

-
 

Attachments

  • SLICICA.jpg
    SLICICA.jpg
    15.1 KB · Views: 389
Last edited:
Physics news on Phys.org
What have you tried? Where are you stuck? Show us your work so far.
 

Similar threads

Calculate the distance the sled travels
  • · Replies 1 ·
Replies
1
Views
2K
Attempt to jump across a river on a motorcycle
  • · Replies 2 ·
Replies
2
Views
4K
Projectile Motion on a Slope: Calculating Distance Traveled
  • · Replies 6 ·
Replies
6
Views
4K
Calculate initial speed of an athlete - projectile motion
  • · Replies 15 ·
Replies
15
Views
4K
Calculating Acceleration of a Ball Rolling Down a Slope
  • · Replies 5 ·
Replies
5
Views
3K
What is the Ideal Angle for a Frog's Jump to Reach 3 Meters Horizontally?
  • · Replies 19 ·
Replies
19
Views
3K
Super fun projectile motion ski slope problem
  • · Replies 1 ·
Replies
1
Views
4K
Speed - the bus jump in the movie
  • · Replies 2 ·
Replies
2
Views
13K
Ski Jump Problem: Find the Distance Down the Slope
  • · Replies 3 ·
Replies
3
Views
11K
Calculate Velocity from Cliff Jump: Horizontal and Vertical Distance
  • · Replies 2 ·
Replies
2
Views
2K