Noman Rasheed
- 29
- 1
So, there is a problem given, where diatomic ideal gas N2 is involved. Both blocks have same volume: 1m3. The molar mass of gas is: 28 g/mol. Initial temperature is 300K.
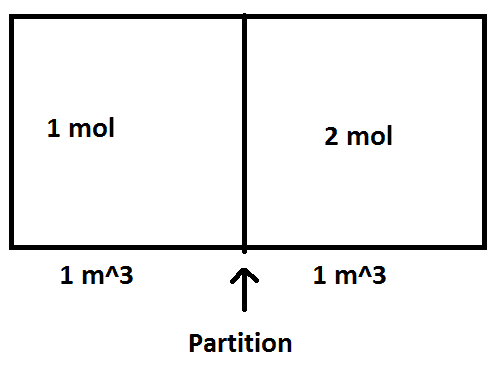
I need to find ΔS and PF.
First, I did find P1 by using formula: PV = nRT
so, P1 = 1*8.3145*300/1 = 2494.35 Pa
and P2 = 2*8.3145*300/1 = 4988.7 Pa
Finally: I have total moles = 3, and total V = 2 m3.
What should I consider next?
I need to find ΔS and PF.
First, I did find P1 by using formula: PV = nRT
so, P1 = 1*8.3145*300/1 = 2494.35 Pa
and P2 = 2*8.3145*300/1 = 4988.7 Pa
Finally: I have total moles = 3, and total V = 2 m3.
What should I consider next?
