skg94
- 78
- 0
Homework Statement
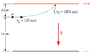
An electron traveling 1.3*10^2m/s enters the region between two parallel plates at the distances shown. When it collides with the plates, it has a speed of 1.8*10^3 m/s. What is the electric field between the plates? What is the electrostatic force on the electron? And how far along the plate does the electron hit?
------- +
|3.0cm (3cm between electron and top plate (positive)
|
electron
|
|
|10cm distance between electron and negative (bottom plate)
------------- negative
Homework Equations
The Attempt at a Solution
I tried using V= ΔE/q but than realized that i probably had to use E = ΔV/ΔD
I really don't know how to go about this. You don't have to give me all the answers, just some steps please