Calculating Electric Field at the Center of a Charged Hemisphere

[Saitama]

Homework Statement

I have to find the electric field at the center of a hemisphere of radius R with charge density σ.

Homework Equations

The Attempt at a Solution

The easiest way would be to select a ring element of small thickness, find the electric field due to it and integrate.
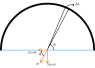
I am trying to do it by an another method. Let's select a small element of area dA subtending a solid angle dΩ at the center, then
$$dA=(dΩ)R^2$$
Charge of this small element is σdA=σ(dΩ)R^2.
Therefore, electric field due to this element is
$$dE=\frac{kσ(dΩ)R^2}{R^2}$$
The last job is to resolve the electric field into two components (see attachement) and integrate them separately but i am stuck here. I can't proceed after this because of the cosθ and sinθ.

 

[gneill]

Your solid angle differential element dΩ would need to be swept over the surface of the hemisphere. But this is not something that's inherent in the formalism for the solid angle element; you would need to impose "direction" of the element via some other mathematical mechanism, and you won't be integrating over dΩ...

Why not make your differential area out of a square patch $(R d\theta)\times(R d\phi)$ where $\theta$ and $\phi$ vary to cover the hemisphere? Use symmetry arguments to simplify the calculation (certain components of the field elements dE will cancel over the integration so they can be dropped).

 

[Saitama]

Your solid angle differential element dΩ would need to be swept over the surface of the hemisphere. But this is not something that's inherent in the formalism for the solid angle element; you would need to impose "direction" of the element via some other mathematical mechanism, and you won't be integrating over dΩ...

Do you have a link (except wiki) which explains this in a simple way? I am not too much familiar with solid angles.

Why not make your differential area out of a square patch $(R d\theta)\times(R d\phi)$ where $\theta$ and $\phi$ vary to cover the hemisphere? Use symmetry arguments to simplify the calculation (certain components of the field elements dE will cancel over the integration so they can be dropped).

Assuming $\theta$ for the lateral surface of hemisphere and $\phi$ for semicircle, how do you get $(R d\theta)\times(R d\phi)$. What i get is an expression like this: $(R\sin\phi d\theta)\times(R d\phi)$. (see attachment)

 

[gneill]

Do you have a link (except wiki) which explains this in a simple way? I am not too much familiar with solid angles.

Sorry, I can't think of a website offhand. Maybe the Wolfram Mathworld site will have something.

Assuming $\theta$ for the lateral surface of hemisphere and $\phi$ for semicircle, how do you get $(R d\theta)\times(R d\phi)$. What i get is an expression like this: $(R\sin\phi d\theta)\times(R d\phi)$. (see attachment)

Yeah, you're right. The latitude influences the length of the arc of longitude for spherical coordinates. So the area element looks like

$dA = R^2 sin(\phi) d\theta d\phi$

 

[Saitama]

Yeah, you're right. The latitude influences the length of the arc of longitude for spherical coordinates. So the area element looks like

$dA = R^2 sin(\phi) d\theta d\phi$

I am myself confused now.
It should be $R\cos\phi$ instead of $R\sin\phi$

 

[gneill]

Ah, well for spherical coordinates the usual practice is to take the angle $\phi$ between the z-axis and the radial vector, rather than between the x-y plane and the vector.

 

[Saitama]

Ah, well for spherical coordinates the usual practice is to take the angle $\phi$ between the z-axis and the radial vector, rather than between the x-y plane and the vector.

I am not aware of spherical coordinate system.
But is my expression for differential area correct?

 

[gneill]

I am not aware of spherical coordinate system.
But is my expression for differential area correct?

It's fine for the appropriate choice of angles. Set up the integration of the resulting field elements. Again, take advantage of symmetry to simplify the calculation.

 

[Saitama]

It's fine for the appropriate choice of angles. Set up the integration of the resulting field elements. Again, take advantage of symmetry to simplify the calculation.

Here's my attempt:
$$dA=R^2\cos(\phi)d\theta d\phi$$
$$dq=σR^2\cos(\phi)d\theta d\phi$$
$$dE=\frac{kdq}{R^2}$$
$$dE=kσR^2\cos(\phi)d\theta d\phi$$
We need to integrate only the sin component because the cos component cancels due to symmetry of the situation.
$$dE\sin(\phi)=\frac{1}{2}kσ\sin(2\phi)d\theta d\phi$$
Integrating this, i get E=0.

 

[gneill]

What were the limits of your integration?

 

[Saitama]

$\phi$ from 0 to $\pi$ and $\theta$ from 0 to $2\pi$.

 

[gneill]

$\phi$ from 0 to $\pi$ and $\theta$ from 0 to $2\pi$.

Ah. You've made your $\phi$ cover the area twice, once from the x-y plane up to the zenith, and then from the zenith back down to the plane. Remember that the $\theta$ will swing the vector all the way around (since it's going from 0 to $2\pi$), so at any given $\phi$ elevation it will already be swept around the whole surface. Make $\phi$ go from 0 to $\pi/2$.

 

[Saitama]

Ah. You've made your $\phi$ cover the area twice, once from the x-y plane up to the zenith, and then from the zenith back down to the plane. Remember that the $\theta$ will swing the vector all the way around (since it's going from 0 to $2\pi$), so at any given $\phi$ elevation it will already be swept around the whole surface. Make $\phi$ go from 0 to $\pi/2$.

Oh yes, i get it. I have got the right answer. Thanks a lot gneill.

This method is way easier than selecting a small ring element.

 

[gneill]

Glad it worked out. Cheers.