Jacob87411
- 170
- 1
Radio waves of wavelength 250 meters from a star reach a radio telescope by two separate paths. One is a direct path to the receiver which is situated on the edge of a cliff by the ocean. The second is by reflection off the water. The first minimum of destructive interference occurs when the star is 25 degrees above the horizon. Find the height of the cliff.
We know the path difference is 125 meters since first minimum occurs at 25 degrees, so the difference is half a wavelength.
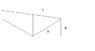
I attached a picture for the rest as a rough diagram (Use the second one)
The distance that ray 2 travels is going to be d - x, which equals 125 meters. The angle there is the 25 the ray is reflecting at, the other two angles are 90 and 65. I am having a real hard time finding H now though, I've figured this all out but can't finish it
We know the path difference is 125 meters since first minimum occurs at 25 degrees, so the difference is half a wavelength.
I attached a picture for the rest as a rough diagram (Use the second one)
The distance that ray 2 travels is going to be d - x, which equals 125 meters. The angle there is the 25 the ray is reflecting at, the other two angles are 90 and 65. I am having a real hard time finding H now though, I've figured this all out but can't finish it