Calculating magnetic induction in a triangle

[diredragon]

Homework Statement

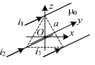
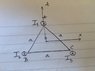
Three very long parallel conductors situated in the air make a direct-symmetrical 3-Phase system. The conductors pass through the A B C points of the triangle of side $a$. The currents in the conductor form a direct-symmetrical 3-Phase system. Effective values of currents are $I$ and the frequency is $w$. The phase of current 1 is $Ψ_1 = 0$.
a) Calculate the vector of magnetic induction $B$ in the point $O$.
b) What does that vector inscribe over time?

Homework Equations

3. The Attempt at a Solution [/B]
The currents in a 3-Phase direct system have a relation
$I_1 = I_m\cos {wt} = I\sqrt2\cos {wt}$
$I_2 = I_m\cos (wt - 2\pi/3) = I\sqrt2\cos (wt - 2\pi/3)$
$I_3 = I_m\cos (wt + 2\pi/3) = I\sqrt2\cos (wt + 2\pi/3)$

Magnetic Induction of a very long straight wire is $B=\frac{μ_0I}{2\pi r}$
The distance of every wire to the point $O$ is $r = \frac{a}{2\sqrt2}$
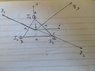
From the wires we only get $B_z$ and $B_x$ since $B_y = 0$. The angles to the axis is $\pi/4$ (This I assumed).
$B_1 = \frac{\sqrt2μ_0I\sqrt2\cos {wt}}{\pi a}$
$B_2 = \frac{\sqrt2μ_0I\sqrt2\cos (wt - 2\pi/3)}{\pi a}$
$B_3 = \frac{\sqrt2μ_0I\sqrt2\cos (wt + 2\pi/3)}{\pi a}$
Total $B_x$ should then be:
$B_x = B_2*\sqrt2/2 + B_3*\sqrt2/2 - B_1*\sqrt2/2$ and $B_z$:
$B_z = B_1*\sqrt2/2 + B_3*\sqrt2/2 - B_2*\sqrt2/2$
Inserting: $B_x = \frac{\sqrt2μ_0I\sqrt2\cos (wt - 2\pi/3)}{\pi a}*\sqrt2/2 + \frac{\sqrt2μ_0I\sqrt2\cos (wt + 2\pi/3)}{\pi a}*\sqrt2/2 - \frac{\sqrt2μ_0I\sqrt2\cos {wt}}{\pi a}*\sqrt2/2$, $B_y = \frac{\sqrt2μ_0I\sqrt2\cos {wt}}{\pi a}*\sqrt2/2 + \frac{\sqrt2μ_0I\sqrt2\cos (wt + 2\pi/3)}{\pi a}*\sqrt2/2 - \frac{\sqrt2μ_0I\sqrt2\cos (wt - 2\pi/3)}{\pi a}*\sqrt2/2$

This seems overly complicated and doesn't seem to match the solution which is simple

Did i assume wrongly that the angle is $\frac{\pi}{4}$. The angle of $\frac{\pi}{6}$ has $\sqrt3$ and that could result in this $\sqrt6$ shown in the answer. Or is it something else?

 

[kuruman]

It looks like you have drawn the magnetic field vectors incorrectly. They should be perpendicular to the vector from each wire to the center of the triangle, not perpendicular to the side of the triangle.

 

[diredragon]

It looks like you have drawn the magnetic field vectors incorrectly. They should be perpendicular to the vector from each wire to the center of the triangle, not perpendicular to the side of the triangle.

You mean like this?

 

[kuruman]

Yes. Remember that the magnetic field lines form circles centered at the wire that generates them. Therefore, at the point of interest they are tangent to the circle and perpendicular to the radius.

 

[diredragon]

Yes. Remember that the magnetic field lines form circles centered at the wire that generates them. Therefore, at the point of interest they are tangent to the circle and perpendicular to the radius.

Right, i was drawing circles on the original picture but i drew the lines incorrectly. What about the other work I've done? Besides the angles, does everything else seems fine?

 

[kuruman]

Everything else should be OK if you figure out the revised vector components correctly.

 

[diredragon]

Everything else should be OK if you figure out the revised vector components correctly.

So with the correct angles, $B_2, B_3$ form a $2\pi/3$ angle with the x-axis and the $B_1$ is it's own projection on the negative x-axis part.
$B_x = B_21/2 + B_31/2 - B_1$ and this equals $\frac{-3μ_0I\cos (wt)}{\pi a}$ according to Wolfram Alpha simplification of the above expression. I am missing a $\frac {\sqrt6}{4}$ term somehow.

 

[kuruman]

You have made a mistake somewhere in your algebra. It pays to be systematic and use a single symbol for a whole bunch of constants that are common to all terms. For example, I rewrote $B_1 = \frac{\sqrt2μ_0I\sqrt2\cos {\omega t}}{\pi a}$ as $B_1 = B_0 \cos \omega t$ where $B_0 = \frac{\sqrt2 μ_0I\sqrt2}{\pi a}$ and the same with the other two. I then used the identity $\cos(a+b)=\cos a ~\cos b-\sin a~\sin b$ to get rid of the $2\pi/3$ phases and have terms in $\cos \omega t$ multiplied by factors like $\pm \frac{1}{2}$ or $\pm \frac{\sqrt{3}}{2}$. Finally, I noted that a given field is parallel (in the clockwise direction) to the triangle side opposite to the wire that generates it. This allowed me to write unit vectors for each field. For example, I found that
$$\vec{B}_2=B_0 \left( -\frac{1}{2}\cos \omega t+\frac{\sqrt{3}}{2}\sin \omega t \right) \left( \frac{1}{2}\hat{x}+\frac{\sqrt{3}}{2} \hat{z} \right)$$
and similar expressions for the other two fields. Adding all three gave the desired result.

 

[diredragon]

You have made a mistake somewhere in your algebra. It pays to be systematic and use a single symbol for a whole bunch of constants that are common to all terms. For example, I rewrote $B_1 = \frac{\sqrt2μ_0I\sqrt2\cos {\omega t}}{\pi a}$ as $B_1 = B_0 \cos \omega t$ where $B_0 = \frac{\sqrt2 μ_0I\sqrt2}{\pi a}$ and the same with the other two. I then used the identity $\cos(a+b)=\cos a ~\cos b-\sin a~\sin b$ to get rid of the $2\pi/3$ phases and have terms in $\cos \omega t$ multiplied by factors like $\pm \frac{1}{2}$ or $\pm \frac{\sqrt{3}}{2}$. Finally, I noted that a given field is parallel (in the clockwise direction) to the triangle side opposite to the wire that generates it. This allowed me to write unit vectors for each field. For example, I found that
$$\vec{B}_2=B_0 \left( -\frac{1}{2}\cos \omega t+\frac{\sqrt{3}}{2}\sin \omega t \right) \left( \frac{1}{2}\hat{x}+\frac{\sqrt{3}}{2} \hat{z} \right)$$
and similar expressions for the other two fields. Adding all three gave the desired result.

Yup, that gave the correct result. Thank you for that clarification.