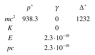Calculating Minimum Energy for Relativistic Collision of Proton and Photon

[joriarty]

Homework Statement

Consider the following reaction that is possible when a proton (p⁺) collides with a photon (γ):
p⁺ + γ → ∆⁺.

Suppose that the photon is a cosmic microwave-background (CMB) photon of energy 2.3 × 10⁻⁴eV. Calculate the minimum energy that the proton must have for this reaction to take place. m_∆ = 1232eV/c².

Hints:

• The minimum energy will be for a head-on collision. Be careful with the signs of the momenta when doing the calculation.

• The answer is a very large energy, so you will be able to make the approximation that the the proton energy is much bigger than it’s rest energy.

• You might find it interesting to look up Greisen-Zatsepin-Kuzmin limit. (is this relevant?)

Homework Equations

K = E − mc²
E² −(pc)² =(mc²)²

The Attempt at a Solution

(See attached table)

I am thinking that because I'm after the minimum energy of the proton for a head on collision, would this mean that the delta baryon is going to have zero kinetic energy and momentum thus a total energy 1232 MeV?

I can then say that the proton has momentum pc = -2.3*10^-10MeV. But that just makes the energy of the proton also equal to 938.3 MeV within the precision of my calculator. That's not right, I should get E_proton>>m_protonc².

Where to now? Does the change in mass of 293.7 MeV have anything to do with this?

Thanks!

 

[Dick]

The GZK limit is very relevant, that's what this whole problem is about. The 10^(-4)ev CMB photon energy is it's energy in the 'lab' frame, one at rest with respect to the CMB background. If you consider the collision in the center of momentum frame of a highly energetic proton, the photon will be 'doppler shifted' up to a high enough energy to produce a delta. You want the energy of the proton in the 'lab' frame.