Calculating Moment of Inertia at Point A

[asi123]

Homework Statement

Hey guys.
So I got this circle (full circle), and I need to find the moment of inertia in point A.
So, of curse I use the parallel axis theorem.
The thing that got me confuse is what's m (in the pic), I mean, it should be the mass at point A, right?
so why, in the examples I saw, they choose it to be the mass of entire circle?
10x.

Homework Equations

The Attempt at a Solution

 

[Doc Al]

The thing that got me confuse is what's m (in the pic), I mean, it should be the mass at point A, right?

What does "mass at point A" mean? You are finding the moment of inertia about point A, which makes sense, but "mass at point A" does not.

so why, in the examples I saw, they choose it to be the mass of entire circle?

Better review the parallel axis theorem. The "m" stands for the mass of the object--the entire object.

 

[asi123]

What does "mass at point A" mean? You are finding the moment of inertia about point A, which makes sense, but "mass at point A" does not.

Better review the parallel axis theorem. The "m" stands for the mass of the object--the entire object.

Lets take an example (in the pic).
First of all, is this correct?
If it is, why do we take the mass that at point A (m) but in the first example, we took the mass of the entire object (M)?
10x.

 

[Doc Al]

Lets take an example (in the pic).
First of all, is this correct?

I cannot tell if it's correct, since I don't know what problem you're trying to solve.

If it is, why do we take the mass that at point A (m) but in the first example, we took the mass of the entire object (M)?

In this diagram it looks like you have two objects. A small one at point A and the disk itself. Are you trying to find the moment of inertia of this two-body system about some axis?

In your first diagram there was only the disk with mass M. There was no other object at point A. (At least I didn't see one and you didn't mention one.)

Please describe the complete problem that you are trying to solve.

 

[asi123]

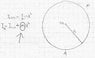
Ok, here is a good example.
I translated it from Hebrew, so sorry for the typing mistakes.
we have a disk with radius R and mass M. The disk is on a table with no friction and the axis goes through the center of the disk. Over the first disk, there's another disk with radius r with no mass. On the upper disk (r), wrapped a string with no mass, and it's connected to a spring, with a spring constant K, and the other end of the spring is connected to the wall. Now, they throw mass m with velocity V_0 (as you can see in the pic) which hits the disk at point A with an angle alpha. The hit is completely not elastic, and the mass m sticks to the disk. as a result of the collision, the system performs an harmonic motion, shown by the equation I put in the red box in the pic.
Ok, that was long , now for the question, the first part is to find the amplitude, this one I actually solved using conservation of Angular Momentum and then conservation of energy.
The second part is the problematic one, at least for me, I need to find the period time (T) of the movement. (BTW the solution there, is there solution, not mine). I think the took the axis, from the top point, the hitting point, other wise, T wouldn't be vertical to R, and the sum of momentum would be zero, right? and also the momentum of inertia, I marked in the green box, which takes us back to our subject, what does this expression means? is this the momentum of inertia at point A?
I know it's a lot of reading, and I'll really appreciate if you help me with this one.
10x guys.

 

[Doc Al]

I think the took the axis, from the top point, the hitting point, other wise, T wouldn't be vertical to R, and the sum of momentum would be zero, right?

The only axis of rotation in this problem is the one in the center of the disks.

and also the momentum of inertia, I marked in the green box, which takes us back to our subject, what does this expression means? is this the momentum of inertia at point A?

It's just the moment of inertia of the system about the central axis: The moment of inertia of the disk (½MR²) plus the moment of inertia of the mass (mR²).

 

[asi123]

But if you choose the center to be the axis, doesn't it mean that R is parallel to the force T and the cross product is zero? and that makes the momentum zero?

 

[Doc Al]

But if you choose the center to be the axis, doesn't it mean that R is parallel to the force T and the cross product is zero?

Only at one point in the oscillation. (When θ = 0.)

and that makes the momentum zero?

You mean (I presume) that the torque and the resulting angular acceleration will be zero at that point, not the angular momentum. But the torque is proportional to the angle. Deviate from θ = 0 and the spring exerts a restoring torque.

The system rotates about a fixed axis, so there really isn't another reasonable choice of axis in this problem.

 

[asi123]

Only at one point in the oscillation. (When θ = 0.)

You mean (I presume) that the torque and the resulting angular acceleration will be zero at that point, not the angular momentum. But the torque is proportional to the angle. Deviate from θ = 0 and the spring exerts a restoring torque.

The system rotates about a fixed axis, so there really isn't another reasonable choice of axis in this problem.

Thanks.