Iqish
- 8
- 1
- Homework Statement
- A thin, homogeneous, curved rod with
the radius of curvature 𝑅 and mass 𝑚 are in
𝑥𝑦 plane. Determine the moment of inertia,
𝐼𝑥'𝑥 ', with respect to the 𝑥 'axis, which goes
through the body's center of mass G
- Relevant Equations
- Steiners sats:𝐼𝑥𝑥 = 𝐼𝑥′𝑥′ + 𝑚𝑦^2𝐺
Given:Thin, homogeneous, curved rod with radius of curvature 𝑅 See figure to the down.
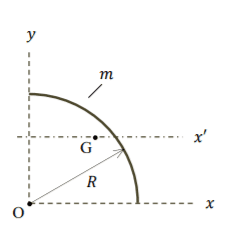
Find: The moment of inertia 𝐼𝑥′𝑥 ′ with respect to 𝑥′- the axis passing through the center of mass (point 𝐺).
Can someone who can help me ?
Find: The moment of inertia 𝐼𝑥′𝑥 ′ with respect to 𝑥′- the axis passing through the center of mass (point 𝐺).
Can someone who can help me ?