Kerrigoth
- 14
- 1
Let's say I place two different size conducting loops inside of a uniform magnetic field. For the sake of the diagram I have the loops share a point, but just treat them as though they are not touching.
Then I decrease the value of the magnetic field very quickly.
\frac{dB}{dt} = \frac{1.6T}{0.3s}=5.3 T/s
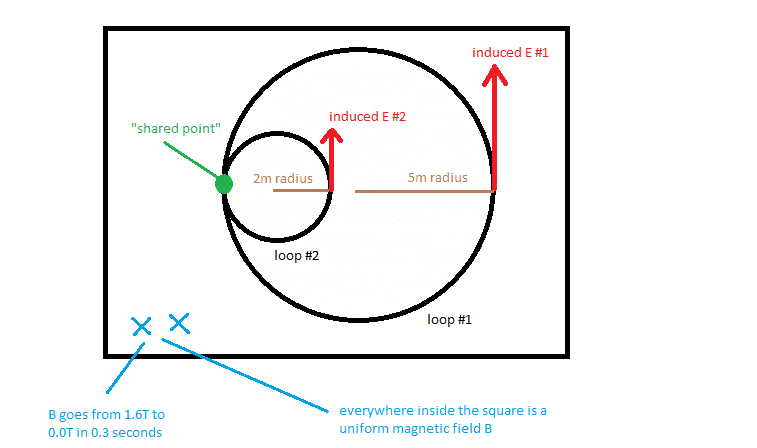
Since I changed the magnitude of the uniform magnetic field, the magnetic flux going through both loops will change. According to Faraday's Law, both loops will experience induced EMFs due to the change in magnetic flux. This will result in current.
\frac{d\Phi _{m}}{dt} = A \frac{dB}{dt} = \epsilon
\epsilon_{1} = \pi (5)^2 \cdot(5.3) = 416.26V \hspace{2cm}<br /> \epsilon_{2} = \pi (2)^2 \cdot(5.3) = 66.6V
Regardless of whether the loops are actually present or not, the changing magnetic field will create an induced electric field.
\epsilon = \oint E\cdot ds = E \cdot2\pi r \hspace{2cm}<br /> E=\frac{\epsilon}{2\pi r}
E_{1} =\frac{416.26}{2\pi (5)} = 13.25 V/m \hspace{2cm}<br /> E_{2} =\frac{66.6 }{2\pi (2)} = 5.3V/m
But the magnitudes of calculated electric fields are bugging me for two reasons:
1) At the "shared point", I have two different calculated values for the electric field. The electric field at a single point can't have two different magnitudes though! I must be doing something inherently wrong in this problem.
2) Judging by my two calculated electric fields: the strength of an induced field increases as the loop's radius increases. For some reason I keep telling myself that the electric field strength should decrease to satisfy some inverse square law. Is there a more intuitive way to look at this that could help overcome my bad instinct?
Then I decrease the value of the magnetic field very quickly.
\frac{dB}{dt} = \frac{1.6T}{0.3s}=5.3 T/s
Since I changed the magnitude of the uniform magnetic field, the magnetic flux going through both loops will change. According to Faraday's Law, both loops will experience induced EMFs due to the change in magnetic flux. This will result in current.
\frac{d\Phi _{m}}{dt} = A \frac{dB}{dt} = \epsilon
\epsilon_{1} = \pi (5)^2 \cdot(5.3) = 416.26V \hspace{2cm}<br /> \epsilon_{2} = \pi (2)^2 \cdot(5.3) = 66.6V
Regardless of whether the loops are actually present or not, the changing magnetic field will create an induced electric field.
\epsilon = \oint E\cdot ds = E \cdot2\pi r \hspace{2cm}<br /> E=\frac{\epsilon}{2\pi r}
E_{1} =\frac{416.26}{2\pi (5)} = 13.25 V/m \hspace{2cm}<br /> E_{2} =\frac{66.6 }{2\pi (2)} = 5.3V/m
But the magnitudes of calculated electric fields are bugging me for two reasons:
1) At the "shared point", I have two different calculated values for the electric field. The electric field at a single point can't have two different magnitudes though! I must be doing something inherently wrong in this problem.
2) Judging by my two calculated electric fields: the strength of an induced field increases as the loop's radius increases. For some reason I keep telling myself that the electric field strength should decrease to satisfy some inverse square law. Is there a more intuitive way to look at this that could help overcome my bad instinct?