vaxop
- 10
- 0
Pressure on a roof (help!)
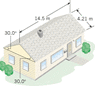
A house has a roof (colored gray) with the dimensions shown in the drawing. Determine the magnitude and direction of the net force that the atmosphere applies to the roof when the outside pressure rises suddenly by 10.0 mm of mercury, before the pressure in the attic can adjust.
ive been on this for hours and i can't figure it out
A house has a roof (colored gray) with the dimensions shown in the drawing. Determine the magnitude and direction of the net force that the atmosphere applies to the roof when the outside pressure rises suddenly by 10.0 mm of mercury, before the pressure in the attic can adjust.
ive been on this for hours and i can't figure it out

Attachments
Last edited: