Anchovy
- 99
- 2
I'm trying to calculate the SU(5) model's prediction for the lower limit of a proton decay lifetime, for the channel p \rightarrow \pi^{0} e^{+}. I'm following this paper:
arXiv:hep-ph/0504276v1
It contains the following equation:
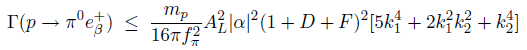
As far as I can tell this actually contains a prediction based also on SO(10), but the paper states that setting k_{2} = 0 means that it reduces to just SU(5).
Anyway, I have the following inputs for this equation and having tried to calculate it in Excel, I end up way away from what I expect to find, which is a proton decaying in 10^{29} - 10^{31} years. Here's what I am using:
$$ k_{1} = \frac{g_{GUT}}{4M_{XY}}, \hspace{0.5 cm}
m_{p} = 938.3 \hspace{1 mm} MeV, \hspace{0.5 cm}
f_{\pi} = 130 \hspace{1 mm} MeV, \hspace{0.5 cm}
A_L = 1.43, \hspace{0.5 cm}
\alpha = 0.003 \hspace{1 mm} GeV^{3}, \hspace{0.5 cm}
D+F = 1.276, \hspace{0.5 cm}
g_{GUT} = 4\pi(\frac{1}{40}), \hspace{0.5 cm}
M_{XY} = 10^{14} \hspace{1 mm} GeV$$
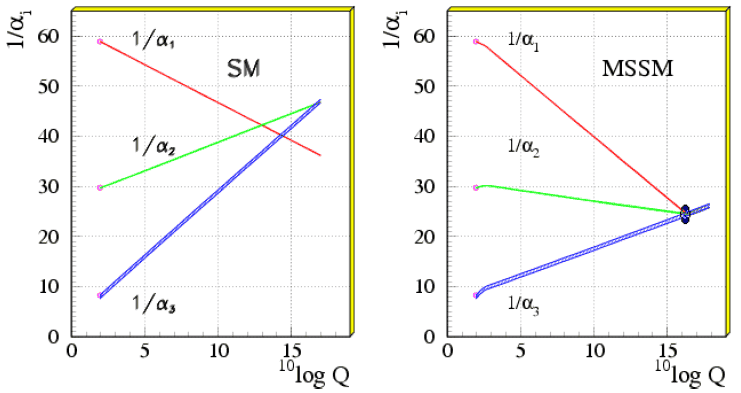
The latter two I have taken from the left plot shown here where I've said \alpha = g / 4\pi:
Anyway, when I compute this, what I find is a number of the order \Gamma \approx 10^{-64}. I assume one then gets the proton lifetime \tau_{p}. by taking \tau_{p} = 1 / \Gamma, but clearly I end up very far away from 10^{29} - 10^{31} years.
I have attached an Excel file where the calculation is broken up into a few steps and they all look fine to me. The final answer I get is shown in bold. Does anyone know what I'm doing wrong? I've tried messing with factors of 1/1000 to make MeV's into GeV's where possible, and also using a factor of (60 * 60 * 24 * 365) seconds per year, but that isn't enough to get me anywhere near the right order of magnitude.
I notice that this equation is different from the rough estimate (according to arXiv:hep-ph/0601023v3) for the proton decay rate:
<br /> \Gamma_{p} \approx \alpha_{GUT}^{2}\frac{m_{p}^{5}}{M_{GUT}^{4}}<br />
where \alpha_{GUT} = g_{GUT} / 4\pi and M_{GUT} \equiv M_{XY} from above if I'm not mistaken. That equation uses the proton mass to the 5th power whereas the long equation above only has m_p to the first power. Overall I'm confused... help?!
Thanks.
arXiv:hep-ph/0504276v1
It contains the following equation:
As far as I can tell this actually contains a prediction based also on SO(10), but the paper states that setting k_{2} = 0 means that it reduces to just SU(5).
Anyway, I have the following inputs for this equation and having tried to calculate it in Excel, I end up way away from what I expect to find, which is a proton decaying in 10^{29} - 10^{31} years. Here's what I am using:
$$ k_{1} = \frac{g_{GUT}}{4M_{XY}}, \hspace{0.5 cm}
m_{p} = 938.3 \hspace{1 mm} MeV, \hspace{0.5 cm}
f_{\pi} = 130 \hspace{1 mm} MeV, \hspace{0.5 cm}
A_L = 1.43, \hspace{0.5 cm}
\alpha = 0.003 \hspace{1 mm} GeV^{3}, \hspace{0.5 cm}
D+F = 1.276, \hspace{0.5 cm}
g_{GUT} = 4\pi(\frac{1}{40}), \hspace{0.5 cm}
M_{XY} = 10^{14} \hspace{1 mm} GeV$$
The latter two I have taken from the left plot shown here where I've said \alpha = g / 4\pi:
Anyway, when I compute this, what I find is a number of the order \Gamma \approx 10^{-64}. I assume one then gets the proton lifetime \tau_{p}. by taking \tau_{p} = 1 / \Gamma, but clearly I end up very far away from 10^{29} - 10^{31} years.
I have attached an Excel file where the calculation is broken up into a few steps and they all look fine to me. The final answer I get is shown in bold. Does anyone know what I'm doing wrong? I've tried messing with factors of 1/1000 to make MeV's into GeV's where possible, and also using a factor of (60 * 60 * 24 * 365) seconds per year, but that isn't enough to get me anywhere near the right order of magnitude.
I notice that this equation is different from the rough estimate (according to arXiv:hep-ph/0601023v3) for the proton decay rate:
<br /> \Gamma_{p} \approx \alpha_{GUT}^{2}\frac{m_{p}^{5}}{M_{GUT}^{4}}<br />
where \alpha_{GUT} = g_{GUT} / 4\pi and M_{GUT} \equiv M_{XY} from above if I'm not mistaken. That equation uses the proton mass to the 5th power whereas the long equation above only has m_p to the first power. Overall I'm confused... help?!
Thanks.
Attachments
Last edited: