Calculating Rx for a 0 Reading on Voltmeter - Ohm's and Kirchhoff's Laws

[lendav_rott]

Homework Statement

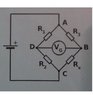
In the diagram, attached to this post, what is the value of Rx in relation to R1 R2 and R3 so that the voltmeter would show 0?

Homework Equations

Ohm's law and Kirchhoff's laws I suppose.

The Attempt at a Solution

I have thought about this thing for too much now, and I have no idea what is going on. My 1st attempt was to use current distribution according to Kirchhoff's current law and see where that takes me, BUT I don't understand how the current flows.
Is it
ABC, ABDC and ADC, ADBC or does it stay looping ABDA(although I doubt it does)?

 

[phinds]

Think about it as two voltage dividers that you want to divide by equal amounts.

 

[lendav_rott]

Ok so for the voltmeter to show 0, the potential difference between B and D is 0, and the potential difference is 0 when the same voltage flows through either side?

So if V1 is my ingoing voltage and V_a and V_b as the 2 equal portions so that their sum would give V1 then
Va = V1*R2/R1+R2
Vb = V1*Rx/Rx+R3

and some simple maths here and there Rx = R2*R3/R1
Thanks for mentioning the voltage division thing, that made it all plain and simple all of a sudden :D amazing how difficultly simple some things can be. So this is just a matter of interpretation of the Ohm's law. Guess that answers my original question of how the current flows too now hmm :)

 

[phinds]

Ok so for the voltmeter to show 0, the potential difference between B and D is 0, and the potential difference is 0 when the same voltage flows through either side?

yep (except that voltage doesn't "flow" --- current does that; sloppy terminology leads to sloppy thinking)

So if V1 is my ingoing voltage and V_a and V_b as the 2 equal portions so that their sum would give V1 then
Va = V1*R2/R1+R2
Vb = V1*Rx/Rx+R3

and some simple maths here and there Rx = R2*R3/R1

I didn't check your math but you certainly have the right idea.

Thanks for mentioning the voltage division thing, that made it all plain and simple all of a sudden :D amazing how difficultly simple some things can be.

Exactly. We all have those moments.

So this is just a matter of interpretation of the Ohm's law.

Not "interpretation", "application". Again, sloppy terminology ...

Guess that answers my original question of how the current flows too now hmm :)

yep

 

[lendav_rott]

Okay I will try to refrain from making these stupid errors.
How would it be acceptable then?
"the potential difference is 0 when the same voltage is present on either side"?
Or how can I say it?
I am only asking because English is not my 1st language.