decaf14
- 23
- 7
Hello,
I would like to replicate the results from the paper "wireless power transfer via strongly coupled magnetic resonances", but I'm having trouble interpreting their equations. I'm creating a MATLAB script to do so. In the paper, they get to a point where L and C are to be calculated in a self-resonating inductor. The equation is of the followng form:
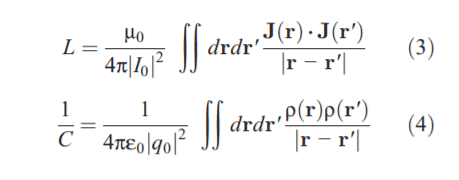
Where J(r) is the spatial current density and p(r) is the charge current density. I'm confused on how to get spatial current density and charge current density. Previously, they mention that "the time dependent current profile has the form I0 * cos(pi * s / L) exp(i * w * t) where I0 is (I'm assuming) current input, s is a "parameterization coefficient" whatever that means (all i know is it varies in value from -l/2 to l/2 so it gives you the spatial location on the coil). "i" is imaginary number 1, L is total length, and t is time.
They jump right from this time dependent current profile into equations 3 and 4 I've listed above. Because they did not discuss methods for calculating J(r), I'm assuming the solution is trivial. However, I do not know where to even start for calculating J(r). Theoretical electromagnetics is not my strong suit. Any help would be greatly appreciated.
EDIT: to clarify a bit more, I understand that current density is simply current / area. However, the current varies at every point in space along the coil. The authors indicate that current is a function of radius, but previously they denote it as being a function of length or time, not radius. If it were to be a function of space, then time would need to be fixed. Even then, it should be a function of length, not radius, according to the equation they have given.
The paper can be found here: https://science.sciencemag.org/content/317/5834/83
I would like to replicate the results from the paper "wireless power transfer via strongly coupled magnetic resonances", but I'm having trouble interpreting their equations. I'm creating a MATLAB script to do so. In the paper, they get to a point where L and C are to be calculated in a self-resonating inductor. The equation is of the followng form:
Where J(r) is the spatial current density and p(r) is the charge current density. I'm confused on how to get spatial current density and charge current density. Previously, they mention that "the time dependent current profile has the form I0 * cos(pi * s / L) exp(i * w * t) where I0 is (I'm assuming) current input, s is a "parameterization coefficient" whatever that means (all i know is it varies in value from -l/2 to l/2 so it gives you the spatial location on the coil). "i" is imaginary number 1, L is total length, and t is time.
They jump right from this time dependent current profile into equations 3 and 4 I've listed above. Because they did not discuss methods for calculating J(r), I'm assuming the solution is trivial. However, I do not know where to even start for calculating J(r). Theoretical electromagnetics is not my strong suit. Any help would be greatly appreciated.
EDIT: to clarify a bit more, I understand that current density is simply current / area. However, the current varies at every point in space along the coil. The authors indicate that current is a function of radius, but previously they denote it as being a function of length or time, not radius. If it were to be a function of space, then time would need to be fixed. Even then, it should be a function of length, not radius, according to the equation they have given.
The paper can be found here: https://science.sciencemag.org/content/317/5834/83
Last edited: