- #1
mertcan
- 340
- 6
Hi, initially I would like to share this link related to derivation of maxwell equation : http://www.physicspages.com/tag/amperes-law/
My question is : in this link, it states interesting situation in electrodynamics is one where the current density
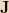 is constant in time, but the charge density
is constant in time, but the charge density
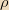 isn’t. I do not understand this sentence, because if current density is constant then current should be constant which means steady state current exist, therefore divergence of J should be 0 which means charge density is constant in time but link does not say so (1 ST QUESTİON)
isn’t. I do not understand this sentence, because if current density is constant then current should be constant which means steady state current exist, therefore divergence of J should be 0 which means charge density is constant in time but link does not say so (1 ST QUESTİON)
, also as a example of it's statement it gives the example of charging capacitor, but in this situation current varies with time which means not constant current and current density. (2 ND QUESTİON)
Besides, if you look at deeply in the link biot savart law is used (applicable to steady currents) not jefimenko equation and after the curl is taken over biot savart, it says divergence of J is not 0 (equal to charge density change over time) , I mean although biot savart rule exist when steady state currents exist, (for the expansion of curl of biot savart) link says divergence of J is not 0. HOW ARE THESE POSSIBLE??
My question is : in this link, it states interesting situation in electrodynamics is one where the current density
, also as a example of it's statement it gives the example of charging capacitor, but in this situation current varies with time which means not constant current and current density. (2 ND QUESTİON)
Besides, if you look at deeply in the link biot savart law is used (applicable to steady currents) not jefimenko equation and after the curl is taken over biot savart, it says divergence of J is not 0 (equal to charge density change over time) , I mean although biot savart rule exist when steady state currents exist, (for the expansion of curl of biot savart) link says divergence of J is not 0. HOW ARE THESE POSSIBLE??
Last edited: