Calculating surface normal vector

AI Thread Summary
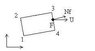
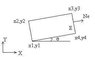
To calculate the normal vector for surface F, the discussion emphasizes the importance of understanding the angle θ between the normal vector Nf and the velocity component U. It is noted that the normal component of U can be derived using the formula Ucosθ, eliminating the need for the absolute normal vector in certain cases. The conversation highlights that in a two-dimensional context, the normal vector can be determined by the negative reciprocal slope of the vector it is normal to, but specific coordinates or angles are required for precise calculations. The user seeks a formula for calculating the unit normal vector for surface F at a given angle, particularly in a Cartesian coordinate system. Clarification on the definition of surface F and specific examples is requested to provide a more accurate response.
andykol
Messages
9
Reaction score
0
Hello,
I am trying to calculate normal vector for surface F Nf (see attached picture) to calculate velocity component for U. I tried to get more info but got confused.
Please tell me how I can calculate Nf.
Thanks in advance.
 

Attachments

  • Vector.JPG
    Vector.JPG
    3.1 KB · Views: 639
Mathematics news on Phys.org
Welcome to PF!

Hello andykol! Welcome to PF! :smile:
andykol said:
I am trying to calculate normal vector for surface F Nf (see attached picture) to calculate velocity component for U. I tried to get more info but got confused.

I'm not sure what you're asking :confused: …

you don't need the normal vector …

to calculate the normal component for U, all you need is the angle, θ, between Nf and U …

the normal component of U is simply Ucosθ. :wink:
 
More information is necessary. In any coordinate system, a vector normal to another vector has a dot product of 0 with that vector. In 2 dimensions, this simplifies to the normal vector having the negative reciprocal slope of the vector it is normal to. you haven't given two-dimensional coordinates to the points, nor angles, so there is no way to calculate an absolute normal vector, but if the problem does not relate to any particular coordinate system (ie., there is no potential field; gravity, electromagnetism) then choose a convenient set of coordinates; ie., let that rectangle be horizontal with vertical sides; then the normal vector points along the positive x-axis. You still need the angle between F and N.
 
Thank you for reply.

But I need to calculate unit normal vector for surface F. I am looking for formula that calculates normal vector of surface with any given angle.
 
andykol said:
But I need to calculate unit normal vector for surface F. I am looking for formula that calculates normal vector of surface with any given angle.

Sorry, I still don't understand :confused: …

how is F defined?

do you have a particular example in mind?
 
Hello tiny-tim,

I have attached detailed picture. I have to calculate unit vector for surface-E Ne. For given Cartesian coordinates, how I can calculate surface normal?
E.g. 2D Cartesian mesh- I got surface-E at an angle θ.
 

Attachments

  • Vector.JPG
    Vector.JPG
    5.1 KB · Views: 674
Last edited:

Thread 'What Exactly is Dirac’s Delta Function? - Insight'

Insights auto threads is broken atm, so I'm manually creating these for new Insight articles. In Dirac’s Principles of Quantum Mechanics published in 1930 he introduced a “convenient notation” he referred to as a “delta function” which he treated as a continuum analog to the discrete Kronecker delta. The Kronecker delta is simply the indexed components of the identity operator in matrix algebra Source: https://www.physicsforums.com/insights/what-exactly-is-diracs-delta-function/ by...
View full post »

Thread 'Fermat's Last Theorem'

Fermat's Last Theorem has long been one of the most famous mathematical problems, and is now one of the most famous theorems. It simply states that the equation $$ a^n+b^n=c^n $$ has no solutions with positive integers if ##n>2.## It was named after Pierre de Fermat (1607-1665). The problem itself stems from the book Arithmetica by Diophantus of Alexandria. It gained popularity because Fermat noted in his copy "Cubum autem in duos cubos, aut quadratoquadratum in duos quadratoquadratos, et...
View full post »
Thread 'Imaginary Pythagorus'

Thread 'Imaginary Pythagorus'

I posted this in the Lame Math thread, but it's got me thinking. Is there any validity to this? Or is it really just a mathematical trick? Naively, I see that i2 + plus 12 does equal zero2. But does this have a meaning? I know one can treat the imaginary number line as just another axis like the reals, but does that mean this does represent a triangle in the complex plane with a hypotenuse of length zero? Ibix offered a rendering of the diagram using what I assume is matrix* notation...
View full post »

Similar threads

I Area of an inclined surface with respect to the original surface
Replies
5
Views
5K
A A question about an 'extremal' surface
Replies
7
Views
2K
I Excellent 3D Graphics thing at math3d.org
Replies
7
Views
2K
I Solving simultaneous vector equations
Replies
11
Views
3K
Normal vector of an embedding surface
Replies
1
Views
1K
B Calculating the perfect tennis shot using vectors
Replies
2
Views
2K
Calculating Normal Vectors for 2D Surfaces: A Scientific Approach
Replies
6
Views
3K
Knowing when to decompose weight vector vs. normal vector
Replies
6
Views
2K
I Finance: does the volatility of a stock follow a certain distribution?
Replies
24
Views
4K
I Equation for circle points in 3D
Replies
3
Views
3K

Hot Threads

Recent Insights

Back
Top