st3dent
- 21
- 0
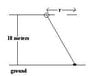
A model plane of mass .75 kg is flying at a constant speed in a horizontal circle connected to a 30 m cord and is at a height of 18 m. The other end of the cord is tethered to the ground as shown in the picture. The plane makes 4.4 revolutions per minute, and the force that the air exerts on the plane is perpendicular to the wings. What is the tension in the cord?
I can see that the ball moves in constant circular motion with r as its radius.
I know that since the ball makes 4.4 revolutions/minute means that the ball has a period(T) of 13.63 seconds.
I also realize that the sum of all forces = ma
As F = ma, Gm1m2/ r2 = ((m)(4 pi2)(r)) / T2
I see that the force of tension (Ft) has an upwards component of Ftsinx that balances the downwards mg and a left component of Ftcosx that directly causes the circular motion.
However, I do not know how to approach this problem.
Where do I start...your help is much appreciated.
I can see that the ball moves in constant circular motion with r as its radius.
I know that since the ball makes 4.4 revolutions/minute means that the ball has a period(T) of 13.63 seconds.
I also realize that the sum of all forces = ma
As F = ma, Gm1m2/ r2 = ((m)(4 pi2)(r)) / T2
I see that the force of tension (Ft) has an upwards component of Ftsinx that balances the downwards mg and a left component of Ftcosx that directly causes the circular motion.
However, I do not know how to approach this problem.
Where do I start...your help is much appreciated.
Attachments
Last edited: