link223
- 70
- 12
- Homework Statement
- Two point charges, and are placed
5.0 cm apart on the x axis. At what points along the x axis is
(a) the electric field zero and (b) the potential zero? Let
V = 0 at r = infinity.
- Relevant Equations
- Electric potential
Apparently, there are two solutions where the electric potential is zero which I don't understand, can I get some input on how this is possible?
I have one thing in mind (which I just thought of and might solve it), the equipotentiality i.e. when I draw a circle for V = 0 around the negative charge it will have 2 points where V = 0 one to the right and one to the left because the equipotential lines are continuous. Is that reasoining correct?
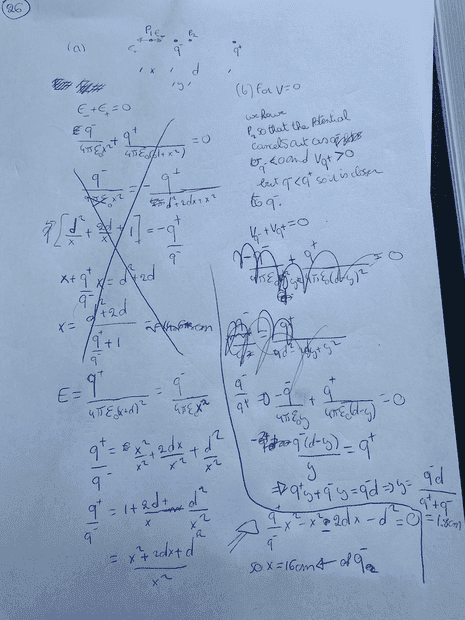
I have one thing in mind (which I just thought of and might solve it), the equipotentiality i.e. when I draw a circle for V = 0 around the negative charge it will have 2 points where V = 0 one to the right and one to the left because the equipotential lines are continuous. Is that reasoining correct?