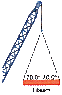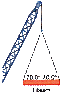rwofford
- 22
- 0
The steel I-beam in the drawing has a weight of 8.90 kN and is being lifted at a constant velocity. What is the tension in each cable attached to its ends? (picture attached)
for this problem do i need to first convert kN to N?...and I am just not sure where to start...
for this problem do i need to first convert kN to N?...and I am just not sure where to start...