Calculating Theta for Fixed Spring Motion

[vladimir69]

hello there
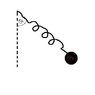
consider a spring that is fixed to a point (i have tried to draw a picture, so to make it clearer as to what i am talking about) that rotates anti clockwise in a horizontal fashion. there is a ball on the end of the spring with mass m, the spring has spring constant k and unstretched length L and the ball moves with angular velocity omega
i am trying to find an expression for theta, the angle that the spring makes with the vertical, as a function of L, w, k, m and g.
me being a maths student and not a physics student just treated this as simaltaneous equations and plugging some stuff together using

W=F*s *cos(theta)
F=m*v^2/L where v is the velocity perpendicular to the centripetal force
F=-k*theta

after a bit of algebra we get that
cos(theta)=-k/(L^2*m*omega^2)
of course one can arrange for theta but i am not sure if this expression is correct, more than likely it is wrong. so if someone could shed some lighton the matter it would be greatly appreciated.

thanks

 

[Doc Al]

Here's how I would approach this problem. Apply Newton's 2nd law to the vertical and horizontal forces on the mass:
T sin\theta = mg, where T is the tension in the spring
T cos\theta = m\omega^2 R, where R is the radius of circle
Combine this with what you know about the spring: its length is L + T/k, thus R = (L + T/k)sin\theta.

You should be able to solve this for for \theta, but it looks messy.

 

[vladimir69]

thanks for the helpful advice