Amrator
- 246
- 83
- Homework Statement
- Train A has proper length ##L##. Train B moves past A (on a parallel track, facing the same direction) with relative speed ##\frac{4c}{5}## (as measured by either train; so each one sees the other move at ##\frac{4c}{5}##). The length of B is such that A says that the fronts of the trains coincide with at exactly the same time as backs coincide. What is the time difference between the fronts coinciding and the backs coinciding, as measured by B? Solve this in two ways: (a) by using length contraction, and (b) by using the rear-clock-ahead effect (among other things).
- Relevant Equations
- $$t_{observed} = \gamma t_{proper}$$
$$L_{observed} = \frac{L_{proper}} {\gamma}$$
$$t_R - t_L = \frac{Lv}{c^2}$$
$$V = \frac{u+v}{1+\frac{uv}{c^2}}$$
a) So I think I solved a. "The length of B is such that A says that the fronts of the trains coincide with at exactly the same time as backs coincide." This tells us that in A's frame, B has the same length as A. So ##L_{observed}## in A's frame is simply ##L##. To obtain the proper length of B, you would then simply multiply ##L## by ##\gamma##. In B's frame, the length of A is contracted by ##\frac{3}{5}##. Now, to obtain the time difference, we subtract the length contraction of A from the proper length of B, and we divide that result by the speed of A. Doing so gives us ##\frac{4L}{3c}##.
b) We have to use the rear-clock-ahead effect which is ##t_R - t_L = \frac{Lv}{c^2}##. The rear-clock-ahead effect basically states that if a train with length ##L## moves with speed##v## relative to you, then you observe the rear clock reading ##\frac{Lv}{c^2}## more than the front clock, at any given instant. So we have to add it to some other time to obtain the time difference. The issue I don't know how to get that time. At the initial time, the front clock will read ##-\frac{Lv}{c^2}##.
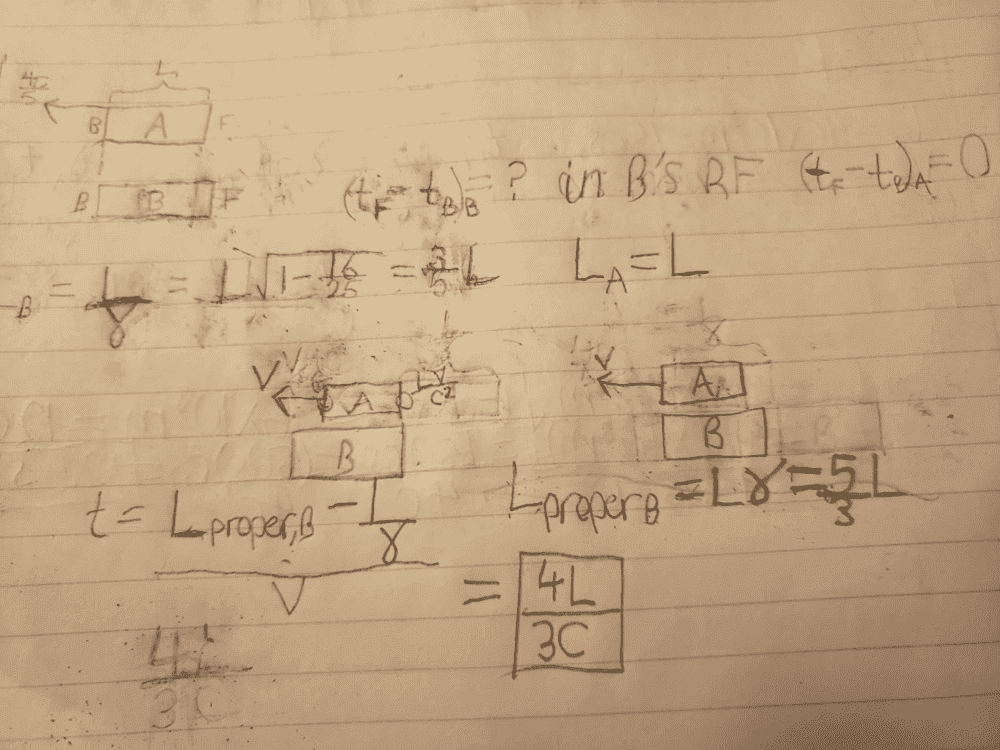
b) We have to use the rear-clock-ahead effect which is ##t_R - t_L = \frac{Lv}{c^2}##. The rear-clock-ahead effect basically states that if a train with length ##L## moves with speed##v## relative to you, then you observe the rear clock reading ##\frac{Lv}{c^2}## more than the front clock, at any given instant. So we have to add it to some other time to obtain the time difference. The issue I don't know how to get that time. At the initial time, the front clock will read ##-\frac{Lv}{c^2}##.
Last edited: