Calculating Travel Time Difference in Optical Fiber | Refraction Homework"

[lvjudge]

Homework Statement

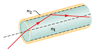
The figure below shows an optical fiber in which a central plastic core of index of refraction n1 = 1.58 is surrounded by a plastic sheath of index of refraction n2 = 1.51. Light can travel along different paths within the central core, leading to different travel times through the fiber. This causes an initially short pulse of light to spread as it travels along the fiber, resulting in information loss. Consider light that travels directly along the central axis of the fiber and light that is repeatedly reflected at the critical angle along the core-sheath interface, reflecting from side to side as it travels down the central core. If the fiber length is 275 m, what is the difference in the travel times along these two routes?

Homework Equations

v=c/n

The Attempt at a Solution

This is my initial failed attempt at a solution
v1=c/n1=189742062
v2=c/n2=198538051.7

The time it takes light traveling at v1 to go 275m:
t1=275/v1=1.449335994E-6 s
The time it takes light traveling at v2 to go 275m:
t2=275/v2=1.385124905E-6 s

delta t=t1-t2=6.421109383E-8=64.21109383 ns
However, this answer was marked incorrect, so i would like so help figuring out how to solve the problem correctly

 

[Redbelly98]

Both paths are in the central fiber of n1=1.58, and thus have the same speed.

Read the question again. Just what is different about the 2 paths?

 

[lvjudge]

Ok, now I see. The first path is just straight through the center. but the second path is reflected off the side of the wire at the critical angle.
I found the critical angle using theta=arcsin(n2/n1)=1.272015952 rad
Now that I've got this information, I really can't figure out where to go or which equation to use. It looks like the variable I need to find is path length for the second path. There's an equation in my textbook from Young's Interference Experiment that states delta L=d sin theta. Is this the one that I should be using?

 

[Redbelly98]

There's an equation in my textbook from Young's Interference Experiment that states delta L=d sin theta. Is this the one that I should be using?

No, this isn't really an interference or diffraction problem.

It's more of a geometry problem. In the figure you gave, find the ratio of the red path to the dashed-line path.