- #1
WherE mE weeD
- 33
- 3
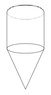
this is a float submerged in fluid the upthrust is greater than the weight. P=ρgh to calculate the pressure should I use the total length of this object as h?
Homework Equations
P=ρgh
Fb=PA (A=area)
The Attempt at a Solution
Curious to know whether I should use the total length of this object in the above equation I'm guessing yes but not too sure.
Which surface area should I input into the buoyancy force equation. The object being less dense than the fluid its submerged in is the reason for the positive buoyancy which makes me think it could be the whole surface area of the object. I'm also thinking the fluid could be compressing the object upwards from the bottom surface because of the difference in densities.
Any advice is appreciated.