odolwa99
- 85
- 0
My answer for part (i) matches up with that of the book but solving for part (ii) has gone awry. Can anyone help me clear this up?
Many thanks.
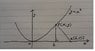
Q. The given diagram (see attachment) shows part of the graph of y = x2. p(x,y) is a point on the curve & a(6,0). bp \perp ab. (i) Express the coordinates of p in terms of x only, (ii) Find the value of x if the area of the triangle abp is a maximum & hence find this maximum area.
(i) If y = x2 => p(x,y) => p(x,x2)
(ii) \frac{1}{2}[(y2 - y1)(x1 - x3) - (x2 - x1)(y1 - y3)] => \frac{1}{2}[(0 - x2)(x - x) - (6 - x)(x2 - 0)] => \frac{1}{2}[0 - (6x2 - x3)] => \frac{1}{2}[-6x2 + x3]
\frac{dA}{dx} = \frac{1}{2}(-12x + 3x2) = 0 => -12x + 3x2 = 0 => 3x2 = 12x => x2 = 4x => x = 4
\frac{d^2A}{dx^2} = \frac{1}{2}(-12 + 6x) => \frac{1}{2}(-12 + 6(4)) => \frac{1}{2} => \frac{1}{2}(12) => 6 > 0, making x = 4 a minimum.
Area = \frac{1}{2}(-6x2 + x3) => \frac{1}{2}(-6(4)2 + 43) => \frac{1}{2}(-96 + 64) => \frac{1}{2}(-32) => -16, i.e. Area is 16
Ans.: (ii) x = 2, Area = 8
Many thanks.
Homework Statement
Q. The given diagram (see attachment) shows part of the graph of y = x2. p(x,y) is a point on the curve & a(6,0). bp \perp ab. (i) Express the coordinates of p in terms of x only, (ii) Find the value of x if the area of the triangle abp is a maximum & hence find this maximum area.
Homework Equations
The Attempt at a Solution
(i) If y = x2 => p(x,y) => p(x,x2)
(ii) \frac{1}{2}[(y2 - y1)(x1 - x3) - (x2 - x1)(y1 - y3)] => \frac{1}{2}[(0 - x2)(x - x) - (6 - x)(x2 - 0)] => \frac{1}{2}[0 - (6x2 - x3)] => \frac{1}{2}[-6x2 + x3]
\frac{dA}{dx} = \frac{1}{2}(-12x + 3x2) = 0 => -12x + 3x2 = 0 => 3x2 = 12x => x2 = 4x => x = 4
\frac{d^2A}{dx^2} = \frac{1}{2}(-12 + 6x) => \frac{1}{2}(-12 + 6(4)) => \frac{1}{2} => \frac{1}{2}(12) => 6 > 0, making x = 4 a minimum.
Area = \frac{1}{2}(-6x2 + x3) => \frac{1}{2}(-6(4)2 + 43) => \frac{1}{2}(-96 + 64) => \frac{1}{2}(-32) => -16, i.e. Area is 16
Ans.: (ii) x = 2, Area = 8