Calculating Wavefunction Angles in sp3 Hybridization - How to Use Integrals?

[Zhelives]

I'm given the following matrix equation:

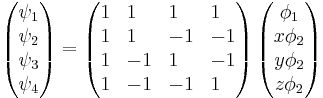
I'm also given:

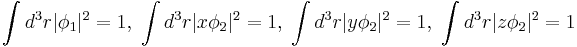
We're supposed to show that the angle between any two of these wave functions is 109.5 (characteristic of sp3 hybridization). I assume I need to calculate the expectation values of x, y and z and then use the dot product, but I'm at a loss on how to evaluate the inegrals. Suggestions?

Thanks.

P.S. Forum Question: Why do the images appear as links when I use the [\IMG] tags?

 

[MaxPolun]

I have a very similar problem myself. I think you need to take the expectation value of two wavefunctions with respect to the position operator. so:
<psi_1|r|psi_1>
since the position is a vector operator you will get a vector quantity. Dot the two of them together, and I'm sure you can get it from there.

btw: how do you get LaTeX to work here?