Calculating Work and Kinetic Energy for Moving Blocks with a Compressed Spring

[xzibition8612]

Homework Statement

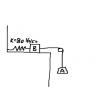
Block A is moving downward at 5 ft/s at a certain time when the spring is compressed 6 inches. The coefficient of friction between block B and the plane is 0.2, the pulley is light, and the weights of A and B are 161 and 193 lb, respectively.

a) Find the distance that A falls from its initial position before coming to zero speed
b) Determine whether or not body A will start to move back upward

Homework Equations

F=ma
W=ΔT
work by spring = (-1/2)(x)

The Attempt at a Solution

The answers are a) 4.78 ft b) A will start back upward

No idea how to start. I suppose I apply F=ma to each A and B separately? Then somehow invoke the work energy equation to figure it out? How do I handle the spring? And the spring compressed 6 inches confuses me. Thanks for the help.

 

[NascentOxygen]

W=ΔT
work by spring = (-1/2)(x)

The energy stored in a spring = ½kx²

As mass A loses potential energy, that energy reappears in the system in other forms. Write the equation that accounts for this. I presume that, since the spring has compressed 6", then the masses have moved the same 6". This should allow you to find the spring constant, k.

(Your sketch shows the spring stretching, whereas I expect it should be drawn as a compression spring.)

Beyond this, I'm afraid I can't help further. I think you'd be looking at a 2nd order DE?